---

0979. 在二叉树中分配硬币

• 标签：树、深度优先搜索、二叉树
• 难度：中等

题目链接

• 0979. 在二叉树中分配硬币 - 力扣

题目大意

描述：

给定一个有 $n$ 个结点的二叉树的根结点 $root$，其中树中每个结点 $node$ 都对应有 $node$.$val$ 枚硬币。整棵树上一共有 $n$ 枚硬币。

在一次移动中，我们可以选择两个相邻的结点，然后将一枚硬币从其中一个结点移动到另一个结点。移动可以是从父结点到子结点，或者从子结点移动到父结点。

要求：

返回使每个结点上「只有」一枚硬币所需的「最少」移动次数。

说明：

• 树中节点的数目为 $n$。
• $1 \le n \le 10^{3}$。
• $0 \le Node.val \le n$。
• 所有 $Node.val$ 的值之和是 $n$。

示例：

• 示例 1：

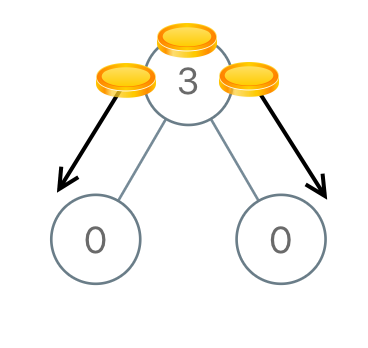
输入：root = [3,0,0]
输出：2
解释：一枚硬币从根结点移动到左子结点，一枚硬币从根结点移动到右子结点。

• 示例 2：

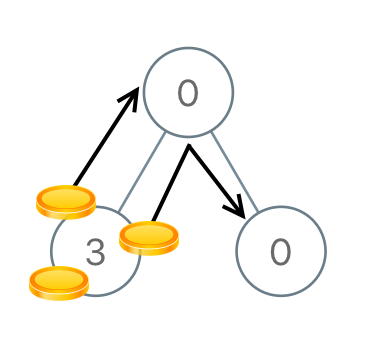
输入：root = [0,3,0]
输出：3
解释：将两枚硬币从根结点的左子结点移动到根结点（两次移动）。然后，将一枚硬币从根结点移动到右子结点。

解题思路

思路 1：深度优先搜索（DFS）

思路

这道题要求计算使每个节点都恰好有一枚硬币所需的最少移动次数。

关键观察：对于每个节点，我们需要计算它的「盈余」或「亏损」：

• 如果一个节点有 $k$ 枚硬币，它需要 $1$ 枚，那么它有 $k - 1$ 枚盈余（或 $k - 1$ 枚亏损）。
• 这些盈余或亏损需要通过父节点传递给其他节点。

我们可以使用后序遍历（先处理子节点，再处理父节点）：

1. 对于每个节点，计算其左右子树的盈余/亏损。
2. 当前节点的盈余 / 亏损 = 左子树盈余 + 右子树盈余 + 当前节点硬币数 - 1。
3. 移动次数 = 所有盈余 / 亏损的绝对值之和（因为每次移动都需要经过边）。

代码

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def distributeCoins(self, root: Optional[TreeNode]) -> int:
        self.moves = 0  # 记录移动次数
        
        def dfs(node):
            """返回当前节点的盈余/亏损"""
            if not node:
                return 0
            
            # 递归处理左右子树
            left_surplus = dfs(node.left)
            right_surplus = dfs(node.right)
            
            # 计算移动次数：左右子树的盈余/亏损都需要通过当前节点传递
            self.moves += abs(left_surplus) + abs(right_surplus)
            
            # 返回当前节点的盈余/亏损
            # = 左子树盈余 + 右子树盈余 + 当前节点硬币数 - 1
            return left_surplus + right_surplus + node.val - 1
        
        dfs(root)
        return self.moves

复杂度分析

• 时间复杂度：$O(n)$，其中 $n$ 是树中节点的数量。每个节点被访问一次。
• 空间复杂度：$O(h)$，其中 $h$ 是树的高度。递归调用栈的深度最多为树的高度。