---

0986. 区间列表的交集

• 标签：数组、双指针、扫描线
• 难度：中等

题目链接

• 0986. 区间列表的交集 - 力扣

题目大意

描述：

给定两个由一些「闭区间」组成的列表，$firstList$ 和 $secondList$，其中 $firstList[i] = [start_i, end_i]$ 而 $secondList[j] = [start_j, end_j]$。每个区间列表都是成对「不相交」的，并且「已经排序」。

要求：

返回这 两个区间列表的交集 。

说明：

• 形式上，闭区间 $[a, b]$（其中 $a \le b$）表示实数 $x$ 的集合，而 $a \le x \le b$。
• 两个闭区间的「交集」是一组实数，要么为空集，要么为闭区间。例如，$[1, 3]$ 和 $[2, 4]$ 的交集为 $[2, 3]$。
• $0 \le firstList.length, secondList.length \le 10^{3}$。
• $firstList.length + secondList.length \ge 1$。
• $0 \le start_i \lt end_i \le 10^{9}$。
• $end_i \lt start_i+1$。
• $0 \le start_j \lt end_j \le 10^{9}$。
• $end_j \lt start_j+1$。

示例：

• 示例 1：

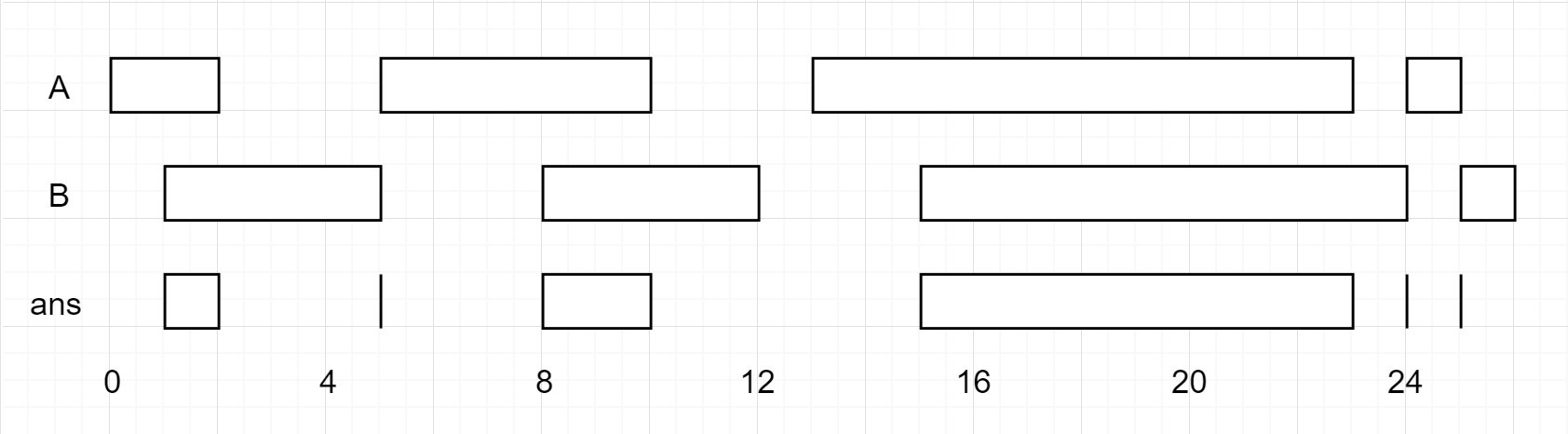
输入：firstList = [[0,2],[5,10],[13,23],[24,25]], secondList = [[1,5],[8,12],[15,24],[25,26]]
输出：[[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]

• 示例 2：

输入：firstList = [[1,3],[5,9]], secondList = []
输出：[]

解题思路

思路 1：双指针

思路

这道题要求找到两个区间列表的交集。我们可以使用双指针分别遍历两个列表：

1. 初始化两个指针 $i$ 和 $j$，分别指向 $firstList$ 和 $secondList$ 的起始位置。
2. 对于当前的两个区间 $[start1, end1]$ 和 $[start2, end2]$：
   • 计算交集：$[\max(start1, start2), \min(end1, end2)]$。
   • 如果交集有效（即 $\max(start1, start2) \le \min(end1, end2)$），将其加入结果。
   • 移动指针：如果 $end1 < end2$，说明第一个区间已经处理完，移动 $i$；否则移动 $j$。
3. 返回所有交集区间。

代码

class Solution:
    def intervalIntersection(self, firstList: List[List[int]], secondList: List[List[int]]) -> List[List[int]]:
        res = []
        i, j = 0, 0
        
        # 双指针遍历两个列表
        while i < len(firstList) and j < len(secondList):
            start1, end1 = firstList[i]
            start2, end2 = secondList[j]
            
            # 计算交集
            start = max(start1, start2)
            end = min(end1, end2)
            
            # 如果交集有效，加入结果
            if start <= end:
                res.append([start, end])
            
            # 移动指针：结束时间较早的区间已经处理完
            if end1 < end2:
                i += 1
            else:
                j += 1
        
        return res

复杂度分析

• 时间复杂度：$O(m + n)$，其中 $m$ 和 $n$ 分别是两个列表的长度。每个区间最多被访问一次。
• 空间复杂度：$O(1)$，不考虑结果数组的空间，只使用了常数个额外变量。