---

0998. 最大二叉树 II

• 标签：树、二叉树
• 难度：中等

题目链接

• 0998. 最大二叉树 II - 力扣

题目大意

描述：

「最大树」定义：一棵树，并满足：其中每个节点的值都大于其子树中的任何其他值。

给你最大树的根节点 $root$ 和一个整数 $val$。

就像 之前的问题 那样，给定的树是利用 Construct(a) 例程从列表 $a$（root = Construct(a)）递归地构建的：

• 如果 $a$ 为空，返回 $null$。
• 否则，令 $a[i]$ 作为 $a$ 的最大元素。创建一个值为 $a[i]$ 的根节点 $root$。
• $root$ 的左子树将被构建为 Construct([a[0], a[1], ..., a[i - 1]])。
• $root$ 的右子树将被构建为 Construct([a[i + 1], a[i + 2], ..., a[a.length - 1]])。
• 返回 $root$。

请注意，题目没有直接给出 $a$，只是给出一个根节点 root = Construct(a)。

假设 $b$ 是 $a$ 的副本，并在末尾附加值 $val$。题目数据保证 $b$ 中的值互不相同。

要求：

返回 Construct(b)。

说明：

• 树中节点数目在范围 $[1, 10^{3}]$ 内。
• $1 \le Node.val \le 10^{3}$。
• 树中的所有值「互不相同」。
• $1 \le val \le 10^{3}$。

示例：

• 示例 1：

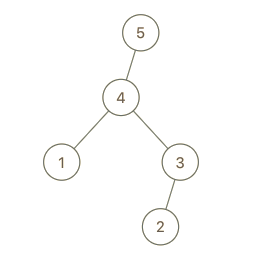
输入：root = [4,1,3,null,null,2], val = 5
输出：[5,4,null,1,3,null,null,2]
解释：a = [1,4,2,3], b = [1,4,2,3,5]

• 示例 2：

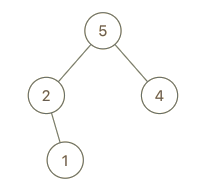
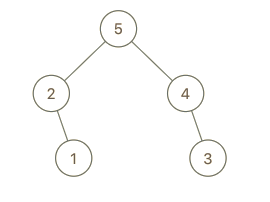
输入：root = [5,2,4,null,1], val = 3
输出：[5,2,4,null,1,null,3]
解释：a = [2,1,5,4], b = [2,1,5,4,3]

解题思路

思路 1：递归

思路

这道题要求在最大二叉树的末尾插入一个新值 $val$。根据最大二叉树的构造规则：

• 如果 $val$ 大于根节点的值，那么 $val$ 应该成为新的根节点，原来的树成为新根的左子树。
• 如果 $val$ 小于根节点的值，那么 $val$ 应该插入到右子树中（因为 $val$ 是在数组末尾添加的）。

我们可以使用递归的方式：

1. 如果当前节点为空，创建一个新节点返回。
2. 如果 $val$ 大于当前节点的值，创建新节点作为根，当前节点作为左子树。
3. 否则，递归地将 $val$ 插入到右子树中。

代码

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def insertIntoMaxTree(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
        # 如果当前节点为空，创建新节点
        if not root:
            return TreeNode(val)
        
        # 如果 val 大于当前节点的值，val 成为新的根节点
        if val > root.val:
            new_root = TreeNode(val)
            new_root.left = root
            return new_root
        
        # 否则，递归地插入到右子树
        root.right = self.insertIntoMaxTree(root.right, val)
        return root

复杂度分析

• 时间复杂度：$O(h)$，其中 $h$ 是树的高度。最坏情况下需要遍历到最右边的叶子节点。
• 空间复杂度：$O(h)$，递归调用栈的深度最多为树的高度。