1.7 归并排序

ITCharge大约 4 分钟

1.7 归并排序

---

1. 归并排序算法思想

归并排序（Merge Sort）基本思想：
利用分治法，将数组递归地一分为二，直至每个子数组只包含一个元素。随后，将这些有序子数组两两合并，最终得到一个整体有序的数组。

2. 归并排序算法步骤

假设数组的元素个数为 $n$ 个，则归并排序的算法步骤如下：

分解过程：递归地将当前数组平分为两部分，直到每个子数组只包含一个元素为止。
1. 找到数组的中间位置 $mid$ ，将数组划分为左、右两个子数组 $left\_nums$ 和 $right\_nums$ 。
2. 分别对 $left\_nums$ 和 $right\_nums$ 递归执行分解操作。
3. 最终将原数组拆分为 $n$ 个长度为 $1$ 的有序子数组。
归并过程：从长度为 $1$ $1$ 的有序子数组开始，逐步将相邻的有序子数组两两合并，最终合并为一个长度为 $n$ $n$ 的有序数组。
1. 新建数组 $nums$ 用于存放合并后的有序结果。
2. 设置两个指针 $left\_i$ 和 $right\_i$ ，分别指向 $left\_nums$ 和 $right\_nums$ 的起始位置。
3. 比较两个指针所指元素，将较小者加入结果数组 $nums$ ，并将对应指针后移一位。
4. 重复上述操作，直到某一指针到达对应子数组末尾。
5. 将另一个子数组剩余的所有元素依次加入结果数组 $nums$ 。
6. 返回合并后的有序数组 $nums$ 。

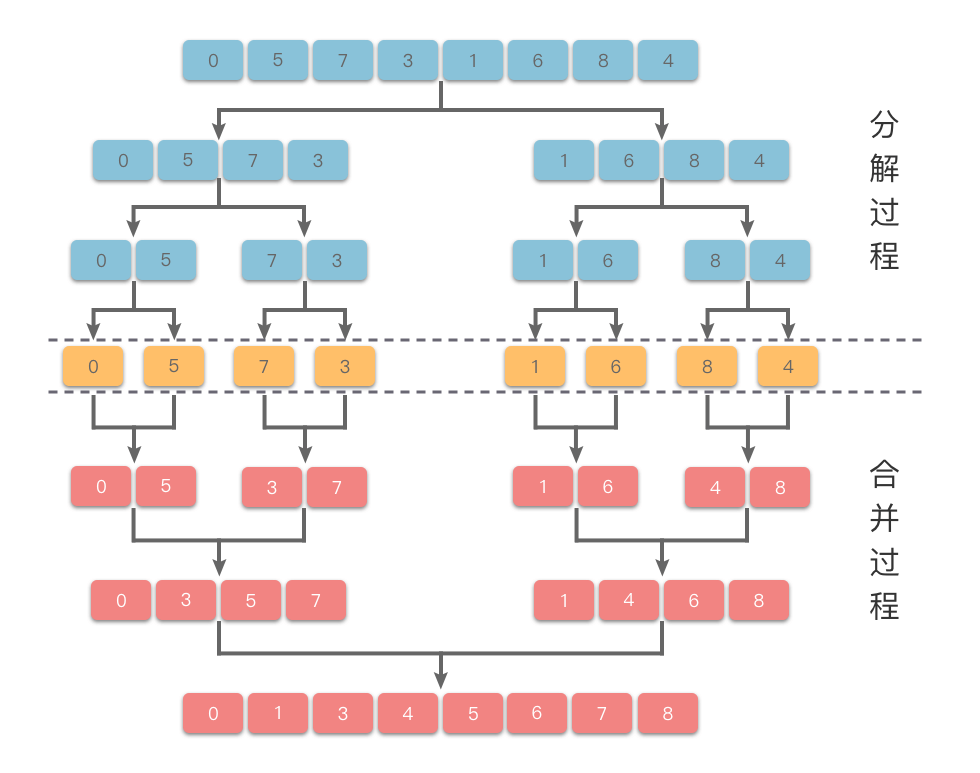
以数组 $[0, 5, 7, 3, 1, 6, 8, 4]$ 为例，演示一下归并排序的算法步骤。

3. 归并排序代码实现

class Solution:
    # 合并过程
    def merge(self, left_nums: [int], right_nums: [int]):
        nums = []
        left_i, right_i = 0, 0
        
        # 合并两个有序子数组
        while left_i < len(left_nums) and right_i < len(right_nums):
            if left_nums[left_i] <= right_nums[right_i]:
                nums.append(left_nums[left_i])
                left_i += 1
            else:
                nums.append(right_nums[right_i])
                right_i += 1
        
        # 如果左子数组有剩余元素，则将其插入到结果数组中
        while left_i < len(left_nums):
            nums.append(left_nums[left_i])
            left_i += 1
        
        # 如果右子数组有剩余元素，则将其插入到结果数组中
        while right_i < len(right_nums):
            nums.append(right_nums[right_i])
            right_i += 1
        
        # 返回合并后的结果数组
        return nums

    # 分解过程
    def mergeSort(self, nums: [int]) -> [int]:
        # 数组元素个数小于等于 1 时，直接返回原数组
        if len(nums) <= 1:
            return nums
        
        mid = len(nums) // 2                        # 将数组从中间位置分为左右两个数组
        left_nums = self.mergeSort(nums[0: mid])    # 递归将左子数组进行分解和排序
        right_nums =  self.mergeSort(nums[mid:])    # 递归将右子数组进行分解和排序
        return self.merge(left_nums, right_nums)    # 把当前数组组中有序子数组逐层向上，进行两两合并

    def sortArray(self, nums: [int]) -> [int]:
        return self.mergeSort(nums)

4. 归并排序算法分析

指标	复杂度	说明
最佳时间复杂度	$O(n \log n)$	无论数组状态如何，都需要 $\log n$ 次分解和 $n$ 次合并
最坏时间复杂度	$O(n \log n)$	无论数组状态如何，都需要 $\log n$ 次分解和 $n$ 次合并
平均时间复杂度	$O(n \log n)$	归并排序的时间复杂度与数据状态无关
空间复杂度	$O(n)$	需要额外的辅助数组来存储合并结果
稳定性	✅ 稳定	合并过程中相等元素的相对顺序保持不变

补充说明：

归并排序采用分治策略，将数组递归地分成两半，每次分解的时间复杂度为 $O(1)$ ，分解次数为 $\log n$ 。
合并过程的时间复杂度为 $O(n)$ ，因为需要遍历两个子数组的所有元素。
总的时间复杂度为 $O(n \log n)$ ，这是基于比较的排序算法的理论下界。

适用场景：

大规模数据排序（ $n > 1000$ ）
对稳定性有要求的场景
外部排序（数据无法全部加载到内存）
链表排序

5. 总结

归并排序是一种高效稳定的排序算法，采用分治策略将数组递归分解后合并排序。

优点：

时间复杂度稳定，始终为 $O(n \log n)$
稳定排序，相等元素相对位置不变
适合大规模数据排序
可用于外部排序和链表排序

缺点：

空间复杂度较高，需要 $O(n)$ 额外空间
对于小规模数据，常数因子较大
不是原地排序算法

1.7 归并排序

1.7 归并排序

1. 归并排序算法思想

2. 归并排序算法步骤

3. 归并排序代码实现

4. 归并排序算法分析

5. 总结

练习题目