3.1 栈基础

---

1. 栈简介

栈（Stack）：也叫做「堆栈」，一种线性表数据结构，只允许在表的一端进行插入和删除操作。

1.1 基本概念

我们可以把栈想象成一摞叠放的盘子：

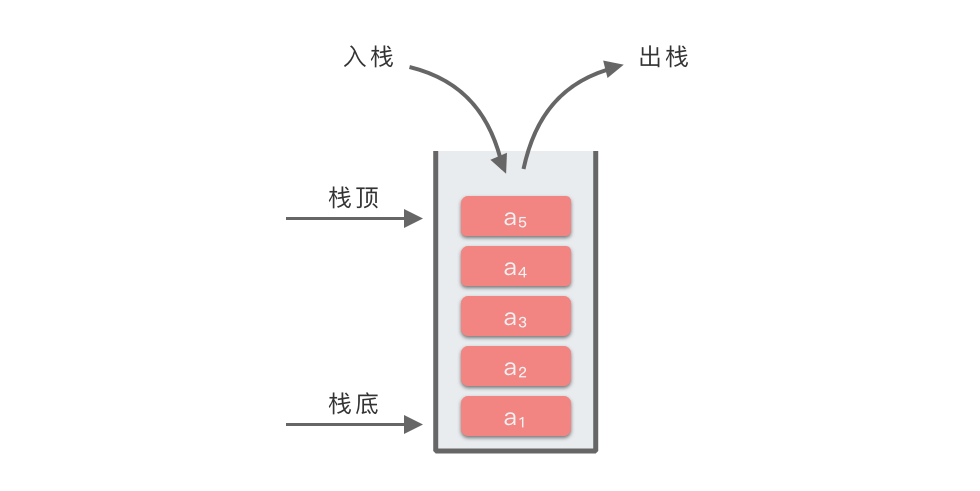
• 栈顶（top）：可以插入和删除元素的一端，就像盘子堆的最上面。
• 栈底（bottom）：固定不动的一端，不能进行操作，就像盘子堆的最下面。
• 空栈：栈中没有任何元素时，称为空栈。

1.2 核心特性

栈的操作遵循 后进先出（LIFO） 的原则：

• 最后放入栈的元素，最先被取出。
• 就像叠盘子，最后放上去的盘子，总是最先被拿走。

1.3 基本操作

栈的常见操作有：

• 入栈（Push）：在栈顶加入一个新元素。
• 出栈（Pop）：移除并返回栈顶的元素。
• 查看栈顶（Peek）：只查看栈顶元素，但不移除。

下图展示了栈的结构和操作方式：

栈结构

2. 栈的实现方式

与线性表类似，栈常见的存储方式有两种：「顺序栈」 和 「链式栈」。

• 顺序栈：采用一段连续的存储空间（如数组）依次存放从栈底到栈顶的元素，并通过指针 $top$ 标记当前栈顶元素在数组中的位置。
• 链式栈：采用单链表实现，每次新元素都插入到链表头部，$top$ 始终指向链表的头节点，即栈顶元素的位置。

2.1 顺序栈（数组实现）

栈的最常见实现方式是利用数组来构建顺序存储结构。在 Python 中，可以直接使用列表（list）来实现顺序栈。

这种基于顺序存储的栈结构，通常被称为 「顺序栈」。

2.1.1 顺序栈的基本描述

栈的顺序存储

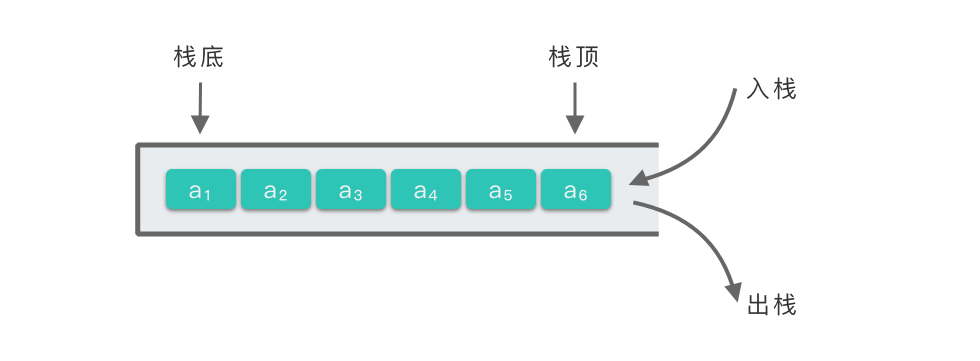
我们约定 $self.top$ 指向当前栈顶元素的位置。

• 初始化空栈：用列表创建空栈，设置栈的最大容量 $self.size$，并将栈顶指针 $self.top$ 设为 $-1$，即 $self.top = -1$。
• 判断栈空：若 $self.top == -1$，则栈为空，返回 $True$，否则返回 $False$。
• 判断栈满：若 $self.top == self.size - 1$，则栈已满，返回 $True$，否则返回 $False$。
• 入栈（push）：先判断栈是否已满，若已满则抛出异常。未满时，将新元素添加到 $self.stack$ 末尾，并将 $self.top$ 加 $1$。
• 出栈（pop）：先判断栈是否为空，若为空则抛出异常。不为空时，删除 $self.stack$ 末尾元素，并将 $self.top$ 减 $1$。
• 获取栈顶元素（peek）：先判断栈是否为空，若为空则抛出异常。不为空时，返回 $self.stack[self.top]$，即栈顶元素。

2.1.2 顺序栈的实现代码

class Stack:
    # 初始化空栈
    def __init__(self, size=100):
        self.stack = []        # 存储元素的数组
        self.size = size       # 栈的最大容量
        self.top = -1          # 栈顶指针，-1表示空栈
    
    def is_empty(self):
        """判断栈是否为空"""
        return self.top == -1
    
    def is_full(self):
        """判断栈是否已满"""
        return self.top + 1 == self.size
    
    def push(self, value):
        """入栈操作"""
        if self.is_full():
            raise Exception('栈已满')
        self.stack.append(value)
        self.top += 1
    
    def pop(self):
        """出栈操作"""
        if self.is_empty():
            raise Exception('栈为空')
        value = self.stack.pop()
        self.top -= 1
        return value
    
    def peek(self):
        """查看栈顶元素"""
        if self.is_empty():
            raise Exception('栈为空')
        return self.stack[self.top]

• 时间复杂度：入栈、出栈、查看栈顶均为 O(1)

2.2 链式栈（链表实现）

栈的链式存储

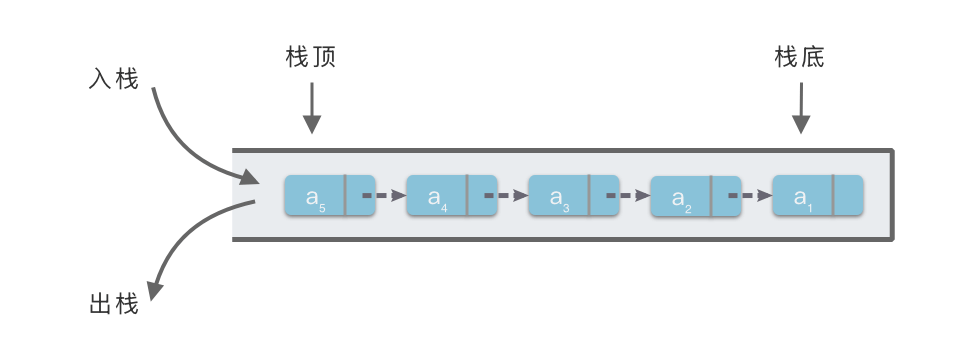
顺序栈在存储空间上存在一定局限性：当栈满或需要扩容时，往往需要移动大量元素，效率较低。为了解决这一问题，可以采用链式存储结构实现栈。在 Python 中，我们通常通过自定义链表节点 $Node$ 来实现链式栈。采用链式存储结构的栈被称为 「链式栈」。

2.2.1 链式栈的基本描述

约定 $self.top$ 始终指向栈顶元素。

• 初始化空栈：将栈顶指针 $self.top$ 设为 $None$，表示栈为空。
• 判断栈是否为空：若 $self.top == None$，则栈为空，返回 $True$，否则返回 $False$。
• 入栈（push）：新建一个值为 $value$ 的链表节点，将其插入到链表头部，并更新 $self.top$ 指向该新节点。
• 出栈（pop）：先判断栈是否为空，若为空则抛出异常。否则，记录当前栈顶节点，$self.top$ 指向下一个节点，并返回原栈顶节点的值。
• 获取栈顶元素（peek）：先判断栈是否为空，若为空则抛出异常。否则，返回 $self.top.value$。

2.2.2 链式栈的实现代码

class Node:
    """链表节点"""
    def __init__(self, value):
        self.value = value     # 节点值
        self.next = None       # 指向下一个节点的指针
        
class Stack:
    def __init__(self):
        """初始化空栈"""
        self.top = None        # 栈顶指针，指向链表头节点
    
    def is_empty(self):
        """判断栈是否为空"""
        return self.top is None
    
    def push(self, value):
        """入栈操作 - 在链表头部插入新节点"""
        new_node = Node(value)
        new_node.next = self.top
        self.top = new_node
    
    def pop(self):
        """出栈操作 - 删除链表头节点"""
        if self.is_empty():
            raise Exception('栈为空')
        value = self.top.value
        self.top = self.top.next
        return value
    
    def peek(self):
        """查看栈顶元素"""
        if self.is_empty():
            raise Exception('栈为空')
        return self.top.value

• 时间复杂度：入栈、出栈、查看栈顶均为 O(1)

2.3 两种实现方式对比

特性	顺序栈	链式栈
空间利用率	固定大小，可能浪费	按需分配，无浪费
扩容操作	需要重新分配空间	无需扩容
内存碎片	较少	可能产生碎片
实现复杂度	简单	相对复杂

3. 栈的经典应用

3.1 经典例题：括号匹配问题

3.1.1 题目链接

• 20. 有效的括号 - 力扣（LeetCode）

3.1.2 题目大意

描述：给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 $s$。

要求：判断字符串 $s$ 是否有效（即括号是否匹配）。

说明：

• 有效字符串需满足：
  1. 左括号必须用相同类型的右括号闭合。
  2. 左括号必须以正确的顺序闭合。

示例：

输入：s = "()"
输出：True


输入：s = "()[]{}"
输出：True

3.2.3 解题思路

思路 1：栈

括号匹配问题是「栈」结构的经典应用场景。我们可以利用栈高效地判断括号是否匹配，具体思路如下：

1. 首先判断字符串长度是否为偶数。由于括号必须成对出现，若长度为奇数，则一定无法完全匹配，直接返回 $False$。
2. 使用栈 $stack$ 存放尚未匹配的左括号。遍历字符串 $s$ 的每个字符，按如下规则处理：
   1. 如果遇到左括号，则将其压入栈中。
   2. 如果遇到右括号，检查栈顶元素是否为对应类型的左括号：
      1. 若匹配，则弹出栈顶元素，继续遍历。
      2. 若不匹配或栈已空，说明括号不合法，直接返回 $False$。
3. 遍历结束后，检查栈是否为空：
   1. 若栈为空，说明所有括号均已正确配对，返回 $True$。
   2. 若栈不为空，说明仍有未配对的左括号，返回 $False$。

思路 1：代码

class Solution:
    def isValid(self, s: str) -> bool:
        # 如果字符串长度为奇数，必然无法完全配对，直接返回 False
        if len(s) % 2 == 1:
            return False
        stack = list()  # 用于存放未配对的左括号
        for ch in s:
            # 如果是左括号，直接入栈
            if ch == '(' or ch == '[' or ch == '{':
                stack.append(ch)
            # 如果是右括号，需要判断栈顶是否为对应的左括号
            elif ch == ')':
                # 栈非空且栈顶为对应的左括号，弹出
                if len(stack) != 0 and stack[-1] == '(':
                    stack.pop()
                else:
                    # 不匹配或栈空，返回 False
                    return False
            elif ch == ']':
                if len(stack) != 0 and stack[-1] == '[':
                    stack.pop()
                else:
                    return False
            elif ch == '}':
                if len(stack) != 0 and stack[-1] == '{':
                    stack.pop()
                else:
                    return False
        # 遍历结束后，栈为空说明全部配对成功
        if len(stack) == 0:
            return True
        else:
            # 栈不为空，说明有未配对的左括号
            return False

思路 1：复杂度分析

• 时间复杂度：$O(n)$。
• 空间复杂度：$O(1)$。

3.2 经典例题：表达式求值问题

3.2.1 题目链接

• 227. 基本计算器 II - 力扣（LeetCode）

3.2.2 题目大意

描述：给定一个字符串表达式 $s$，表达式中所有整数为非负整数，运算符只有 +、-、*、/，没有括号。

要求：实现一个基本计算器来计算并返回它的值。

说明：

• $1 \le s.length \le 3 * 10^5$。
• $s$ 由整数和算符（+、-、*、/）组成，中间由一些空格隔开。
• $s$ 表示一个有效表达式。
• 表达式中的所有整数都是非负整数，且在范围 $[0, 2^{31} - 1]$ 内。
• 题目数据保证答案是一个 32-bit 整数。

示例：

输入：s = "3+2*2"
输出：7


输入：s = " 3/2 "
输出：1

3.2.3 解题思路

思路 1：栈

在表达式计算中，乘除运算优先于加减运算。我们可以优先处理乘除，将结果暂存，再统一处理加减。

具体实现时，可以借助一个栈来保存每一步的中间结果。遇到正数直接入栈，遇到负数则取相反数入栈。这样，最终的计算结果就是栈中所有元素的和。

详细步骤如下：

1. 遍历字符串 $s$，用变量 $op$ 记录当前数字前的运算符，初始为 +。
2. 当遇到数字时，连续读取完整数字 $num$，根据 $op$ 的类型进行如下处理：
   1. 若 $op$ 为 +，将 $num$ 入栈。
   2. 若 $op$ 为 -，将 $-num$ 入栈。
   3. 若 $op$ 为 *，弹出栈顶元素 $top$，计算 $top \times num$，将结果入栈。
   4. 若 $op$ 为 /，弹出栈顶元素 $top$，计算 $int(top / num)$，将结果入栈。
3. 如果遇到运算符 +、-、*、/，则更新 $op$。
4. 最后，将栈中所有数字求和，返回结果。

思路 1：代码

class Solution:
    def calculate(self, s: str) -> int:
        size = len(s)
        stack = []      # 用于存储每一步的中间结果
        op = '+'        # 记录上一个运算符，初始为加号
        index = 0
        while index < size:
            if s[index] == ' ':
                # 跳过空格
                index += 1
                continue
            if s[index].isdigit():
                # 解析多位数字
                num = ord(s[index]) - ord('0')
                while index + 1 < size and s[index+1].isdigit():
                    index += 1
                    num = 10 * num + ord(s[index]) - ord('0')
                # 根据上一个运算符进行处理
                if op == '+':
                    stack.append(num)         # 加号直接入栈
                elif op == '-':
                    stack.append(-num)        # 减号取相反数入栈
                elif op == '*':
                    top = stack.pop()         # 乘法弹出栈顶元素
                    stack.append(top * num)   # 计算后入栈
                elif op == '/':
                    top = stack.pop()         # 除法弹出栈顶元素
                    # Python 的 int() 向零取整，符合题意
                    stack.append(int(top / num))
            elif s[index] in "+-*/":
                # 更新当前运算符
                op = s[index]
            index += 1
        # 栈中所有元素求和即为最终结果
        return sum(stack)

思路 1：复杂度分析

• 时间复杂度：$O(n)$。
• 空间复杂度：$O(n)$。

练习题目

• 0155. 最小栈

• 0020. 有效的括号

• 0227. 基本计算器 II

• 0150. 逆波兰表达式求值

• 0394. 字符串解码

• 0946. 验证栈序列

• 栈基础题目列表

参考资料

• 【书籍】数据结构与算法 Python 语言描述 - 裘宗燕 著
• 【书籍】数据结构教程 第 3 版 - 唐发根 著
• 【书籍】大话数据结构 程杰 著
• 【文章】栈 - 数据结构与算法之美 - 极客时间