4.4 KMP 算法

ITCharge大约 10 分钟

4.4 KMP 算法

---

1. KMP 算法介绍

KMP 算法（全称 Knuth-Morris-Pratt 算法）：由 Donald Knuth、James H. Morris 和 Vaughan Pratt 三位学者于 1977 年联合提出，并以他们的名字命名。
KMP 算法核心思想：在字符串匹配过程中，当文本串 $T$ 的某个字符与模式串 $p$ 发生不匹配时，充分利用已匹配的前缀信息，通过预处理得到的「部分匹配表」（即 next 数组），避免文本指针的回退，从而高效地减少不必要的比较次数，实现快速匹配。

1.1 朴素匹配算法的缺陷

在朴素匹配算法（Brute Force）中，匹配过程使用指针 $i$ 和 $j$ 分别指向文本串 $T$ 和模式串 $p$ 当前比较的字符。当遇到 $T$ 和 $p$ 的字符不匹配时， $j$ 会回到模式串的起始位置， $i$ 则回退到上一次匹配起点的下一个字符，重新开始新一轮匹配，如下图所示。

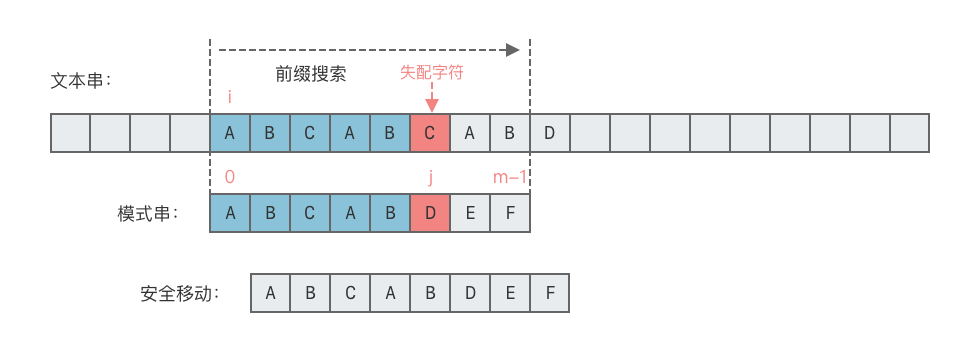
也就是说，每当以 $T[i]$ 为起点的匹配失败后，算法会直接尝试从 $T[i + 1]$ 作为新起点继续匹配。实际上，这种做法导致指针 $i$ 可能频繁回退，造成大量重复比较。

那么，有没有一种算法能够让 $i$ 始终向右移动，无需回退，从而提升匹配效率呢？

1.2 KMP 算法的改进

KMP 算法的核心在于：每次匹配失败时，能够利用已匹配的信息，跳过那些必然无法匹配的位置，从而显著减少无效的比较次数，实现高效匹配。

具体来说，每次失配时，我们已经知道：主串的某一段子串等于模式串的某一前缀。也就是说，如果在下标 $j$ 处失配，说明 $T[i: i + j] == p[0: j]$ ，即主串从 $i$ 开始的前 $j$ 个字符和模式串的前 $j$ 个字符完全相同。

那么，这一信息如何帮助我们加速匹配呢？

以图中例子为例，假设在第 $5$ 个字符处失配，即 $T[i: i + 5]$ 与 $p[0: 5]$ 完全相同（如 "ABCAB" == "ABCAB"），但第 $6$ 个字符不匹配。进一步观察，模式串的前 $5$ 个字符中，前 $2$ 位前缀和后 $2$ 位后缀相同（即 "AB" == "AB"）。

因此，我们可以得出：主串子串的后 $2$ 位（ $T[i + 3: i + 5]$ ）和模式串的前 $2$ 位（ $p[0: 2]$ ）是相同的，这部分已经比较过，无需重复。于是，我们可以直接将主串的 $T[i + 5]$ 与模式串的 $p[2]$ 对齐，继续匹配。这样，主串指针 $i$ 始终向右移动，无需回退，只需调整模式串指针 $j$ 。

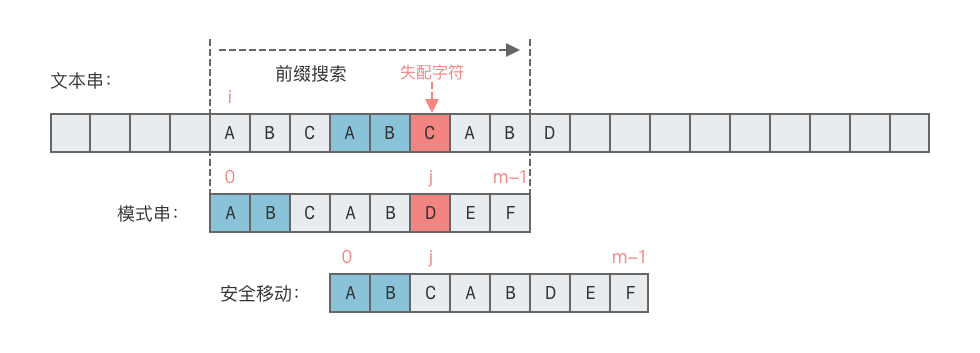
KMP 算法正是基于这种思想，对模式串 $p$ 进行预处理，构建出一个 「部分匹配表」（即 next 数组）。每当失配发生时，主串指针 $i$ 不回退，而是根据 next 数组中 $next[j - 1]$ 的值，直接将模式串指针 $j$ 移动到合适的位置，跳过无效的比较。

例如，上述例子中，模式串在 $j = 5$ 处失配， $next[4] = 2$ ，因此我们将 $j$ 移动到 $2$ ，让 $T[i + 5]$ 直接对齐 $p[2]$ ，继续匹配，无需回退主串指针 $i$ 。

1.3 next 数组

前文提到的「部分匹配表」又称为「前缀表」，在 KMP 算法中用 $next$ 数组来表示。 $next[j]$ 的含义是：记录子串 $p[0: j + 1]$ （包含下标 $j$ ）中，最长的相等前后缀的长度。

换句话说， $next[j]$ 就是：在 $p[0: j + 1]$ 这个子串中，既是前缀又是后缀的最长子串的长度（但不能包含整个子串本身）。

举例说明，设 $p = "ABCABCD"$ ，其 $next$ 数组为：

$next[0] = 0$ ，因为 "A" 没有相同的前后缀。
$next[1] = 0$ ，因为 "AB" 没有相同的前后缀。
$next[2] = 0$ ，因为 "ABC" 没有相同的前后缀。
$next[3] = 1$ ，因为 "ABCA" 的前后缀 "A" 相同，长度为 $1$ 。
$next[4] = 2$ ，因为 "ABCAB" 的前后缀 "AB" 相同，长度为 $2$ 。
$next[5] = 3$ ，因为 "ABCABC" 的前后缀 "ABC" 相同，长度为 $3$ 。
$next[6] = 0$ ，因为 "ABCABCD" 没有相同的前后缀。

同理，"ABCABDEF" 的前缀表为 $[0, 0, 0, 1, 2, 0, 0, 0]$ ，"AABAAAB" 的前缀表为 $[0, 1, 0, 1, 2, 2, 3]$ ，"ABCDABD" 的前缀表为 $[0, 0, 0, 0, 1, 2, 0]$ 。

在前面的例子中，当 $p[5]$ 与 $T[i + 5]$ 匹配失败，根据 $next[4] = 2$ ，我们可以直接将 $T[i + 5]$ 与 $p[2]$ 对齐，继续匹配，如下图所示：

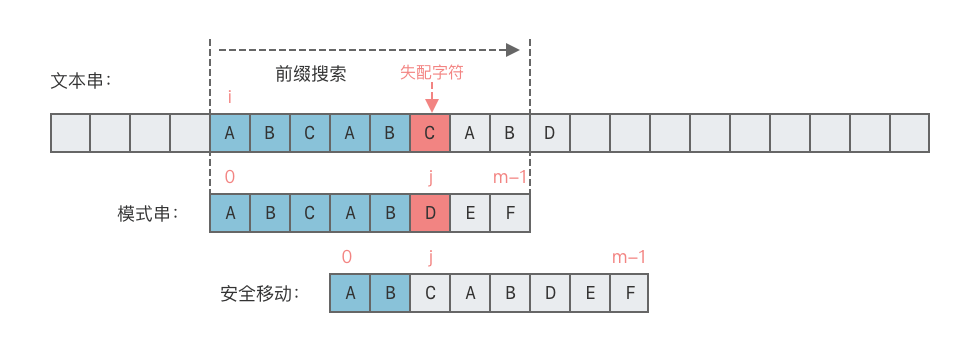
那么，这样移动的原理是什么？

实际上，这正是前缀表的作用。具体来说：

假设在第 $j$ 个字符处失配，即 $T[i: i + j] == p[0: j]$ ，但 $T[i + j] \ne p[j]$ 。此时，如果 $p[0: k] == p[j - k:j]$ ，且 $k$ 最大，则 $T[i + j - k: i + j]$ 与 $p[0: k]$ 已经相等，无需重复比较。

因此，我们可以直接将 $T[i + j]$ 与 $p[k]$ 对齐，继续匹配。这里的 $k$ 就是 $next[j - 1]$ 的值。

简而言之， $next$ 数组帮助我们在失配时，快速定位到模式串中下一个可能匹配的位置，从而避免主串指针回退，大幅提升匹配效率。

2. KMP 算法步骤

2.1 next 数组的构造

$next$ 数组的构建其实很直观：它记录了模式串每个前缀（不包含当前位置）中，最长的“相等前后缀”长度。这样一旦失配，我们就能直接跳到下一个可能的匹配位置，避免重复比较。

具体步骤如下：

假设模式串为 $p$ ，我们用两个指针： $left$ 表示当前已知的最长相等前后缀的长度， $right$ 表示当前正在处理的字符下标。初始时 $left = 0$ ， $right = 1$ 。
比较 $p[left]$ $p [l e f t]$ 和 $p[right]$ $p [r i g h t]$ ：
- 如果 $p[left] == p[right]$ ，说明前后缀可以继续延长。此时 $left$ 加 $1$ ，将 $next[right]$ 设为 $left$ ，然后 $right$ 右移一位。这样， $next[right]$ 就记录了当前最长的相等前后缀长度，方便失配时快速跳转。
- 如果 $p[left] \ne p[right]$ ，说明当前前后缀不相等。此时 $left$ 回退到 $next[left - 1]$ ，即尝试寻找更短的相等前后缀，直到 $left = 0$ 或再次匹配成功为止。 $right$ 不动，继续比较。
重复上述过程，直到 $right$ 遍历完整个模式串。

最终， $next[j]$ 就表示子串 $p[0: j+1]$ 的最长相等前后缀的长度。这个数组就是 KMP 算法高效跳转的关键。

2.2 KMP 算法整体流程

先根据模式串 $p$ 构建其前缀表（即 $next$ 数组）。
设置两个指针： $i$ 指向文本串 $T$ 的当前位置， $j$ 指向模式串 $p$ 的当前位置，初始均为 $0$ 。
遍历文本串 $T$ $T$ ：
- 如果 $T[i] == p[j]$ ，则 $i$ 和 $j$ 同时右移一位，继续比较下一个字符。
- 如果 $T[i] \ne p[j]$ 且 $j > 0$ ，则将 $j$ 回退到 $next[j - 1]$ ，即利用前缀表跳过无效匹配，无需回退 $i$ 。
- 如果 $T[i] \ne p[j]$ 且 $j == 0$ ，则 $i$ 右移一位， $j$ 保持为 $0$ 。
当 $j$ 等于模式串长度 $m$ 时，说明已找到完整匹配，返回匹配的起始下标 $i - m + 1$ 。
如果遍历完整个文本串仍未找到完整匹配，则返回 $-1$ 。

该流程通过 $next$ 数组高效跳转，避免了主串指针的回退，大幅提升了匹配效率。

3. KMP 算法代码实现

# 生成 next 数组
# next[j] 表示子串 p[0: j+1] 的最长相等前后缀的长度
def generateNext(p: str):
    m = len(p)
    next = [0 for _ in range(m)]  # 初始化 next 数组，全部为 0

    left = 0  # left 表示当前已知的最长相等前后缀的长度
    for right in range(1, m):  # right 表示当前考察的字符下标
        # 如果前后缀不相等，尝试回退 left 到更短的前后缀
        while left > 0 and p[left] != p[right]:
            left = next[left - 1]  # 回退到上一个最长相等前后缀
        # 如果前后缀相等，最长相等前后缀长度加一
        if p[left] == p[right]:
            left += 1
        next[right] = left  # 记录当前最长相等前后缀长度
    return next

# KMP 匹配算法，T 为文本串，p 为模式串
def kmp(T: str, p: str) -> int:
    """
    返回模式串 p 在文本串 T 中首次出现的位置（下标），若不存在则返回 -1
    """
    n, m = len(T), len(p)
    if m == 0:
        return 0  # 空模式串视为匹配在开头

    next = generateNext(p)  # 生成 next 数组

    j = 0  # j 为模式串当前匹配到的位置
    for i in range(n):  # i 为文本串当前匹配到的位置
        # 如果当前字符不匹配，且 j > 0，则回退 j 到 next[j-1]
        while j > 0 and T[i] != p[j]:
            j = next[j - 1]
        # 如果当前字符匹配，j 向右移动
        if T[i] == p[j]:
            j += 1
        # 如果模式串全部匹配，返回匹配起始下标
        if j == m:
            return i - m + 1
    return -1  # 未找到匹配，返回 -1

# 测试用例
print(kmp("abbcfdddbddcaddebc", "ABCABCD"))  # 不存在，返回 -1
print(kmp("abbcfdddbddcaddebc", "bcf"))      # 返回 2
print(kmp("aaaaa", "bba"))                   # 不存在，返回 -1
print(kmp("mississippi", "issi"))            # 返回 1
print(kmp("ababbbbaaabbbaaa", "bbbb"))       # 返回 3

4. KMP 算法分析

指标	复杂度	说明
最好时间复杂度	$O(n + m)$	构造前缀表 $O(m)$ ，匹配阶段无回退 $O(n)$ ，总计 $O(n + m)$
最坏时间复杂度	$O(n + m)$	无论文本和模式内容如何，均为 $O(n + m)$
平均时间复杂度	$O(n + m)$	平均情况下同样为 $O(n + m)$
空间复杂度	$O(m)$	仅需存储模式串的前缀表（next 数组）

构造前缀表（ $next$ ）阶段的时间复杂度为 $O(m)$ ，其中 $m$ 是模式串 $p$ 的长度。
匹配阶段根据前缀表调整位置，文本串指针 $i$ 不回退，时间复杂度为 $O(n)$ ，其中 $n$ 是文本串 $T$ 的长度。
因此整体时间复杂度为 $O(n + m)$ ，空间复杂度为 $O(m)$ 。与朴素匹配的 $O(n \times m)$ 相比，有显著提升。

5. 总结

KMP 算法通过预处理模式串的前缀信息，实现文本串指针不回退的高效匹配，是经典的线性时间字符串查找算法。

优点：

匹配阶段线性时间，文本指针不回退，效率稳定。
仅依赖模式串的前缀表，额外空间开销小（ $O(m)$ ）。
缺点：
实现与理解相对复杂，调试成本高于朴素算法。
仅适用于精确匹配；包含通配符、编辑距离等需求需用其他算法（如 Aho–Corasick、DP、后缀结构等）。

练习题目

参考资料

【书籍】柔性字符串匹配 - 中科院计算所网络信息安全研究组译
【书籍】ACM-ICPC 程序设计系列 - 算法设计与实现 - 陈宇吴昊主编
【博文】从头到尾彻底理解 KMP - 结构之法算法之道 - CSDN博客
【博文】字符串匹配的 KMP 算法 - 阮一峰的网络日志
【题解】多图预警 - 详解 KMP 算法 - 实现 strStr() - 力扣
【题解】「代码随想录」KMP算法详解 - 实现 strStr() - 力扣