4.6 Horspool 算法
大约 6 分钟
4.6 Horspool 算法
---1. Horspool 算法介绍
Horspool 算法:由 Nigel Horspool 教授于 1980 年提出,是对 Boyer Moore 算法的简化版,用于在字符串中查找子串。
- Horspool 算法核心思想:先对模式串 预处理,生成移动表。匹配时,从模式串末尾开始比较,遇到不匹配时,根据移动表跳过尽可能多的位置,加快查找速度。
Horspool 算法本质上继承了 Boyer-Moore 的思想,但只保留了「坏字符规则」并加以简化。当文本串 某字符与模式串 不匹配时,模式串可以根据以下两种情况快速右移:
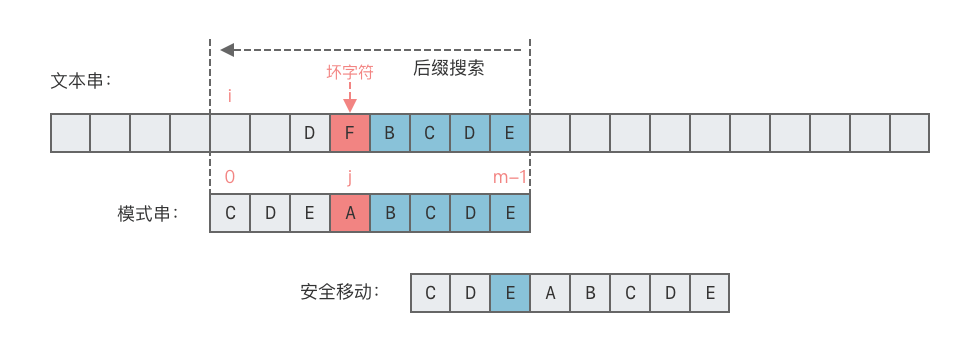
- 情况 1:(文本串当前窗口的最后一个字符)在模式串 中出现过
- 将该字符在模式串中最后一次出现的位置与模式串末尾对齐。
- 右移位数 = 模式串长度 - 1 - 该字符在模式串中最后一次出现的位置
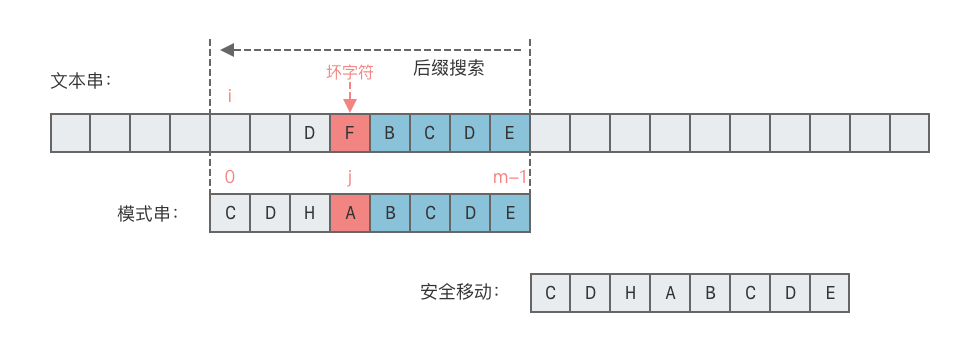
- 情况 2: 没有在模式串 中出现
- 直接将模式串整体右移一整个长度。
- 右移位数 = 模式串长度
2. Horspool 算法步骤
Horspool 算法流程如下:
- 设文本串 长度为 ,模式串 长度为 。
- 预处理模式串 ,生成后移位数表 。
- 从文本串起始位置 开始,将模式串与文本串对齐,比较方式如下:
- 从模式串末尾 开始,依次向前比较 与 。
- 如果全部字符匹配,返回 ,即匹配起始位置。
- 如果遇到不匹配,查找 在 中的值,右移相应距离(如果未出现则右移 )。
- 如果遍历完文本串仍未找到匹配,返回 。
3. Horspool 算法代码实现
3.1 后移位数表代码实现
后移位数表的生成非常简单,类似于 Boyer-Moore 算法的坏字符表:
- 用一个哈希表 ,记录每个字符在模式串中可向右移动的距离。
- 遍历模式串 ,对每个字符 ,将 作为其移动距离存入表中。如果字符重复,保留最右侧的距离。
匹配时,如果 不在表中,则右移 ;如果在表中,则右移 。
后移位数表代码如下:
# 生成后移位数表
# bc_table[bad_char] 表示遇到坏字符时可以向右移动的距离
def generateBadCharTable(p: str):
"""
构建 Horspool 算法的后移位数表。
输入:
p: 模式串
输出:
bc_table: 字典,key 为字符,value 为遇到该字符时可向右移动的距离
"""
m = len(p)
bc_table = dict()
# 只处理模式串的前 m - 1 个字符(最后一个字符不需要处理)
for i in range(m - 1): # i 从 0 到 m - 2
# 对于每个字符 p[i],记录其对应的移动距离
# 移动距离 = 模式串长度 - 1 - 当前字符下标
bc_table[p[i]] = m - 1 - i
# 如果字符重复出现,保留最右侧(下标最大)的距离
return bc_table3.2 Horspool 算法整体代码实现
# Horspool 算法实现,T 为文本串,p 为模式串
def horspool(T: str, p: str) -> int:
"""
Horspool 字符串匹配算法。
返回模式串 p 在文本串 T 中首次出现的位置,如果无则返回 -1。
"""
n, m = len(T), len(p)
if m == 0:
return 0 if n == 0 else -1 # 约定:空模式串匹配空文本串返回 0,否则返回 -1
if n < m:
return -1 # 模式串比文本串长,必不匹配
bc_table = generateBadCharTable(p) # 生成后移位数表
i = 0
while i <= n - m:
j = m - 1
# 从模式串末尾向前逐位比较
while j >= 0 and T[i + j] == p[j]:
j -= 1
if j < 0:
return i # 匹配成功,返回起始下标
# 取文本串当前窗口最右字符,查表决定滑动距离
shift_char = T[i + m - 1]
shift = bc_table.get(shift_char, m) # 如果未出现则右移 m 位
i += shift
return -1 # 匹配失败,未找到
# 生成 Horspool 算法的后移位数表
# bc_table[bad_char] 表示遇到坏字符 bad_char 时可以向右移动的距离
def generateBadCharTable(p: str):
"""
构建 Horspool 算法的后移位数表。
输入:
p: 模式串
输出:
bc_table: 字典,key 为字符,value 为遇到该字符时可向右移动的距离
"""
m = len(p)
bc_table = dict()
# 只处理模式串的前 m - 1 个字符(最后一个字符不处理)
for i in range(m - 1): # i 从 0 到 m - 2
# 对于每个字符 p[i],记录其对应的移动距离
# 移动距离 = 模式串长度 - 1 - 当前字符下标
bc_table[p[i]] = m - 1 - i
# 如果字符重复出现,保留最右侧(下标最大)的距离
return bc_table
# 测试用例
print(horspool("abbcfdddbddcaddebc", "aaaaa")) # -1,未匹配
print(horspool("abbcfdddbddcaddebc", "bcf")) # 2,匹配成功4. Horspool 算法分析
| 指标 | 复杂度 | 说明 |
|---|---|---|
| 最好时间复杂度 | 模式串字符分布均匀,坏字符表能实现最大跳跃,比较次数最少。 | |
| 最坏时间复杂度 | 模式串字符高度重复且与文本不匹配时,每次只能滑动一位。 | |
| 平均时间复杂度 | 实际应用中通常接近最好情况,比较次数较少。 | |
| 空间复杂度 | 主要用于存储坏字符表, 为模式串长度, 为字符集大小。 |
- 为文本串长度, 为模式串长度, 为字符集大小。
- Horspool 算法在大多数实际场景下效率较高,但极端情况下可能退化为 。
- 空间消耗主要体现在坏字符表的构建上。
4. 总结
Horspool 算法是一种基于坏字符规则的高效字符串匹配算法,通过预处理模式串构建坏字符表,实现快速跳跃以提升匹配效率,适用于大多数实际场景。
- 优点:
- 实现简单,代码量少,易于理解。
- 平均性能优良,适合大多数实际应用场景。
- 只需构建坏字符表,预处理开销小。
- 缺点:
- 最坏情况下时间复杂度较高,可能退化为 。
- 只利用坏字符规则,跳跃能力不如 BM 算法。
- 不适合极端重复或特殊构造的模式串。
练习题目
参考资料
- 【书籍】柔性字符串匹配 - 中科院计算所网络信息安全研究组 译
- 【博文】字符串模式匹配算法:BM、Horspool、Sunday、KMP、KR、AC算法 - schips - 博客园