4.8 字典树
4.8 字典树
---1. 字典树介绍
字典树(Trie),又称前缀树,是一种高效存储和查找字符串集合的树形结构。可以把它想象成一本「分层字典」:每个单词从根节点出发,按字母顺序一层层分支,直到单词结尾。具有相同前缀的单词会在树上共用同一条路径,就像家族树中有共同祖先的亲戚一样,这样能大幅提升查找和前缀匹配的效率。
下图展示了一棵字典树,包含 "a"、"abc"、"acb"、"acc"、"ach"、"b"、"chb" 这 7 个单词。
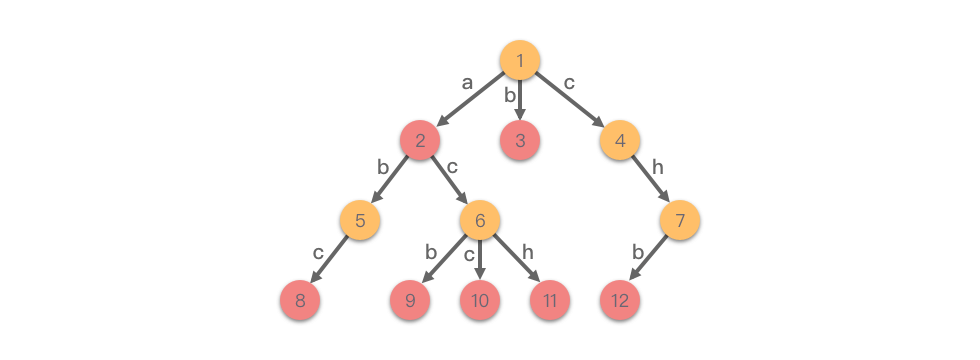
在图中,边表示字符,从根节点到某节点的路径即为一个单词。例如 表示 "acc"。每个单词的结尾节点通常会有一个结束标记 (红色节点),用于区分完整单词。
字典树的本质是利用字符串的公共前缀,将相同前缀的单词合并存储,从而加快查询速度,减少重复比较,利用空间换时间。
字典树的基本性质:
- 根节点不存字符,其他每个节点只存一个字符。
- 从根到某节点的路径组成该节点对应的字符串。
- 每个节点的所有子节点字符都不相同。
2. 字典树的基本操作
字典树常见的基本操作包括 创建、插入、查找 和 删除。其中,删除操作在实际应用中较少用到,因此本节主要聚焦于字典树的创建、插入和查找。
2.1 字典树的结构
2.1.1 字典树节点的定义
我们先明确字典树节点的结构。
字典树本质上是一棵多叉树,即每个节点可以拥有多个子节点。实现多叉结构时,常见的方式有两种:使用数组或哈希表。下面分别介绍这两种实现方式。
- 当字符串仅包含小写英文字母时,可以用长度为 的数组来存储每个节点的所有子节点。例如:
class Node: # 字符节点
def __init__(self):
# 初始化字符节点
# children 是长度为 26 的数组,分别对应 'a'~'z' 的子节点
self.children = [None for _ in range(26)] # 初始化所有子节点为 None
self.isEnd = False # isEnd 用于标记该节点是否为某个单词的结尾上述代码中, 采用数组结构,表示该节点的全部子节点; 用于标记该节点是否为某个单词的结尾。
在插入单词时,需要将每个字符转换为对应的数字索引,然后在长度为 的数组中定位并创建相应的子节点。
- 如果字符集不仅包含小写字母,还包括大写字母或其他字符,则可使用哈希表来存储当前节点的所有子节点,具体实现如下:
class Node: # 字符节点
def __init__(self): # 初始化字符节点
self.children = dict() # 用哈希表存储所有子节点,key 为字符,value 为 Node 实例
self.isEnd = False # 标记该节点是否为某个单词的结尾
# 例如:children['a'] 表示以当前节点为父节点,字符为 'a' 的子节点在上述代码中, 采用哈希表结构,用于存储该节点的所有子节点, 用于标记该节点是否为某个单词的结尾。插入单词时,可以根据单词的每个字符,动态创建对应的字符节点,并将其加入哈希表,便于高效查找和插入。
为统一实现和便于维护,本文后续所有代码均采用哈希表来管理节点的子节点。
2.1.2 字典树的基本结构
在明确了字典树节点的结构后,我们进一步定义字典树的整体结构。字典树在初始化时会创建一个根节点,该根节点不存储任何字符。所有的插入和查找操作均从根节点出发。下面是字典树的基本结构代码:
class Trie: # 字典树(前缀树)
def __init__(self):
"""
初始化字典树,创建一个根节点。
根节点不存储任何字符,仅作为所有单词的公共起点。
"""
self.root = Node() # 初始化根节点(根节点不保存字符)2.2 字典树的创建与插入操作
字典树的「创建」是指将字符串数组中的所有字符串依次插入到字典树中;而「插入」操作则是将单个字符串加入到字典树的过程。
2.2.1 字典树的插入操作
在介绍字典树的批量创建前,先说明单个单词的插入流程:
- 从根节点出发,依次遍历单词的每个字符 (根节点本身不存储字符)。
- 如果当前节点的子节点中不存在字符 ,则新建一个节点
cur.children[ch] = Node(),并将当前指针移动到新节点。 - 如果当前节点的子节点中已存在字符 ,则直接将当前指针移动到该子节点。
- 当所有字符遍历完毕后,将当前节点标记为单词结尾(即
isEnd = True)。
# 向字典树中插入一个单词
def insert(self, word: str) -> None:
"""
将一个单词插入到字典树中。
参数:
word (str): 需要插入的单词
"""
cur = self.root # 从根节点开始
for ch in word: # 遍历单词中的每个字符
# 如果当前节点的子节点中不存在字符 ch,则新建一个节点
if ch not in cur.children:
cur.children[ch] = Node() # 创建新节点并加入子节点字典
# 移动到下一个字符节点,继续插入
cur = cur.children[ch]
# 单词所有字符插入完成后,将当前节点标记为单词结尾
cur.isEnd = True2.2.2 字典树的创建操作
字典树的创建过程比较简单,通常包括以下步骤:
- 先实例化一个字典树对象,如
trie = Trie()。 - 遍历单词列表,将每个单词依次插入到字典树中。
# 创建一个字典树实例
trie = Trie()
# 遍历单词列表,将每个单词插入到字典树中
for word in words:
trie.insert(word)2.3 字典树的查找操作
2.3.1 字典树的查找单词操作
在字典树中查找某个单词是否存在的过程与插入操作类似,具体步骤如下:
- 从根节点出发,依次遍历单词的每个字符 。
- 如果当前节点的子节点中不存在字符 ,则说明该单词不在字典树中,直接返回 。
- 如果存在字符 ,则将当前指针移动到对应的子节点,继续查找下一个字符。
- 当所有字符遍历完毕后,检查当前节点是否被标记为单词结尾(
isEnd = True)。如果是,则说明字典树中存在该单词,返回 ;否则返回 。
# 查找字典树中是否存在一个单词
def search(self, word: str) -> bool:
"""
在字典树中查找指定单词是否存在。
参数:
word (str): 需要查找的单词
返回:
bool: 如果单词存在于字典树中,返回 True;否则返回 False
"""
cur = self.root # 从根节点开始
for ch in word: # 遍历单词中的每个字符
if ch not in cur.children: # 如果当前节点的子节点中不存在该字符
return False # 说明单词不存在,直接返回 False
cur = cur.children[ch] # 移动到对应的子节点,继续查找下一个字符
return cur.isEnd # 所有字符查找完毕,判断当前节点是否为单词结尾标记2.3.2 字典树的查找前缀操作
在字典树中查找某个前缀是否存在,其过程与查找完整单词类似。不同之处在于,查找前缀时只需依次判断每个字符是否存在于相应的子节点中,无需判断最后节点是否为单词结尾标记。只要前缀的所有字符都能顺利匹配,即可认为该前缀存在于字典树中。
# 查找字典树中是否存在一个前缀
def startsWith(self, prefix: str) -> bool:
"""
在字典树中查找指定前缀是否存在。
参数:
prefix (str): 需要查找的前缀字符串
返回:
bool: 如果前缀存在于字典树中,返回 True;否则返回 False
"""
cur = self.root # 从根节点开始
for ch in prefix: # 遍历前缀中的每个字符
if ch not in cur.children: # 如果当前节点的子节点中不存在该字符
return False # 说明前缀不存在,直接返回 False
cur = cur.children[ch] # 移动到对应的子节点,继续查找下一个字符
return True # 所有字符查找完毕,前缀存在于字典树中3. 字典树的实现代码
class Node: # 字符节点(Trie 树的节点)
def __init__(self):
self.children = dict() # 子节点字典,key 为字符,value 为 Node 对象
self.isEnd = False # 是否为单词结尾标记
class Trie: # 字典树(Trie)
def __init__(self):
"""
初始化字典树,创建一个空的根节点(根节点不保存字符)
"""
self.root = Node()
def insert(self, word: str) -> None:
"""
向字典树中插入一个单词
参数:
word (str): 要插入的单词
"""
cur = self.root # 从根节点开始
for ch in word: # 遍历单词中的每个字符
if ch not in cur.children: # 如果当前节点没有ch这个子节点
cur.children[ch] = Node() # 新建一个子节点
cur = cur.children[ch] # 移动到子节点,继续处理下一个字符
cur.isEnd = True # 单词插入完成,标记结尾
def search(self, word: str) -> bool:
"""
查找字典树中是否存在一个完整单词
参数:
word (str): 要查找的单词
返回:
bool: 存在返回True,否则返回False
"""
cur = self.root # 从根节点开始
for ch in word: # 遍历单词中的每个字符
if ch not in cur.children: # 如果没有对应的子节点
return False # 单词不存在
cur = cur.children[ch] # 移动到子节点
return cur.isEnd # 判断是否为单词结尾
def startsWith(self, prefix: str) -> bool:
"""
查找字典树中是否存在某个前缀
参数:
prefix (str): 要查找的前缀
返回:
bool: 存在返回True,否则返回False
"""
cur = self.root # 从根节点开始
for ch in prefix: # 遍历前缀中的每个字符
if ch not in cur.children: # 如果没有对应的子节点
return False # 前缀不存在
cur = cur.children[ch] # 移动到子节点
return True # 前缀存在4. 字典树的算法分析
| 指标 | 复杂度 | 说明 |
|---|---|---|
| 插入一个单词 | 时间: 空间:(数组实现) 空间:(哈希表实现) | 为单词长度, 为字符集大小。数组实现空间消耗大,哈希表实现更节省空间。 |
| 查找一个单词 | 时间: 空间: | 为单词长度,仅遍历单词长度,空间为常数。 |
| 查找一个前缀 | 时间: 空间: | 为前缀长度,仅遍历前缀长度,空间为常数。 |
5. 字典树的应用
字典树一个典型的应用场景就是:在搜索引擎中输入部分内容之后,搜索引擎就会自动弹出一些关联的相关搜索内容。我们可以从中直接选择自己想要搜索的内容,而不用将所有内容都输入进去。这个功能从一定程度上节省了我们的搜索时间。
例如下图,当我们输入「字典树」后,底下会出现一些以「字典树」为前缀的相关搜索内容。

这个功能实现的基本原理就是字典树。当然,像 Google、必应、百度这样的搜索引擎,在这个功能能的背后肯定做了大量的改进和优化,但它的底层最基本的原理就是「字典树」这种数据结构。
除此之外,我们可以把字典树的应用分为以下几种:
- 字符串检索:事先将已知的⼀些字符串(字典)的有关信息存储到字典树⾥, 查找⼀些字符串是否出现过、出现的频率。
- 前缀统计:统计⼀个串所有前缀单词的个数,只需统计从根节点到叶子节点路径上单词出现的个数,也可以判断⼀个单词是否为另⼀个单词的前缀。
- 最长公共前缀问题:利用字典树求解多个字符串的最长公共前缀问题。将⼤量字符串都存储到⼀棵字典树上时, 可以快速得到某些字符串的公共前缀。对所有字符串都建⽴字典树,两个串的最长公共前缀的长度就是它们所在节点最近公共祖先的长度,于是转变为最近公共祖先问题。
- 字符串排序:利⽤字典树进⾏串排序。例如,给定多个互不相同的仅由⼀个单词构成的英⽂名,将它们按字典序从⼩到⼤输出。采⽤数组⽅式创建字典树,字典树中每个节点的所有⼦节点都是按照其字母⼤⼩排序的。然后对字典树进⾏先序遍历,输出的相应字符串就是按字典序排序的结果。
6. 总结
字典树(Trie)是一种高效存储和查找字符串集合的树形数据结构,通过利用字符串的公共前缀来减少重复比较,实现快速的前缀匹配和字符串检索。
优点:
- 查找效率高:查找单词和前缀的时间复杂度均为 ,其中 为字符串长度,比暴力匹配快很多
- 前缀匹配优秀:能够快速判断一个字符串是否为另一个字符串的前缀,这在搜索引擎自动补全等场景中非常有用
- 空间共享:具有相同前缀的单词共享路径,相比单独存储每个单词,能节省大量空间
- 支持动态操作:可以动态插入、删除字符串,适合需要频繁更新的字符串集合
缺点:
- 空间消耗较大:每个节点都需要存储子节点信息,对于稀疏的字符串集合,空间利用率不高
- 实现复杂度:相比简单的哈希表或数组,字典树的实现和维护更加复杂
- 字符集限制:使用数组实现时,字符集大小会影响空间复杂度,大字符集会显著增加内存消耗
- 缓存不友好:树形结构在内存中的分布可能不够连续,对 CPU 缓存不够友好
练习题目
参考资料
- 【书籍】算法训练营 陈小玉 著
- 【书籍】ACM-ICPC 程序设计系列 算法设计与实现 陈宇 吴昊 主编
- 【博文】Trie 树 - 数据结构与算法之美 - 极客时间
- 【博文】一文搞懂字典树
- 【博文】字典树 (Trie) - OI Wiki