5.4 二叉搜索树
大约 9 分钟
5.4 二叉搜索树
---1. 二叉搜索树简介
二叉搜索树(Binary Search Tree, BST),又称二叉查找树、有序二叉树或排序二叉树,是一种特殊的二叉树结构,满足以下性质:
- 对于任意节点,如果其左子树非空,则左子树所有节点的值均 小于 该节点的值;
- 对于任意节点,如果其右子树非空,则右子树所有节点的值均 大于 该节点的值;
- 任意节点的左右子树也都分别是二叉搜索树(递归定义)。
下图展示了三棵典型的二叉搜索树:
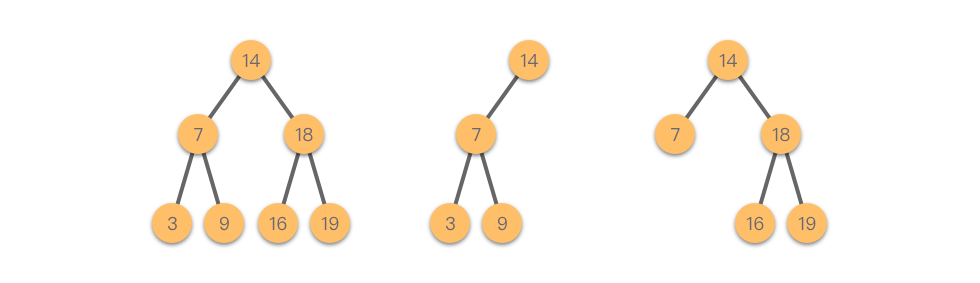
二叉搜索树的核心特性是:左子树所有节点值 < 根节点值 < 右子树所有节点值。
基于这一特性,如果对二叉搜索树进行中序遍历,得到的节点值序列一定是递增的。例如,某棵二叉搜索树的中序遍历结果如下图所示。
2. 二叉搜索树的查找
二叉搜索树查找:即在二叉搜索树中定位值为 的节点。
2.1 查找算法思路
基于二叉搜索树的性质,查找过程可以高效地缩小范围。每次比较后,只需决定向左子树还是右子树继续查找,从而大大提升查找效率。具体步骤如下:
- 如果当前二叉搜索树为空,查找失败,返回空指针 。
- 如果当前节点不为空,将待查找值 与当前节点值 比较:
- 如果 ,查找成功,返回该节点。
- 如果 ,递归查找左子树。
- 如果 ,递归查找右子树。
2.2 查找算法代码实现
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val # 节点值
self.left = left # 左子节点
self.right = right # 右子节点
class Solution:
def searchBST(self, root: TreeNode, val: int) -> TreeNode:
"""
在二叉搜索树中查找值为 val 的节点
参数:
root: TreeNode,二叉搜索树的根节点
val: int,待查找的目标值
返回:
TreeNode,值为 val 的节点,如果未找到则返回 None
"""
if not root:
return None # 空树或查找失败,返回 None
if val == root.val:
return root # 找到目标节点,返回
elif val < root.val:
# 目标值小于当前节点值,递归查找左子树
return self.searchBST(root.left, val)
else:
# 目标值大于当前节点值,递归查找右子树
return self.searchBST(root.right, val)2.3 二叉搜索树的查找算法分析
| 指标 | 复杂度 | 说明 |
|---|---|---|
| 最优时间 | 树接近完全平衡,高度为 ,每次查找缩小一半范围 | |
| 最坏时间 | 树退化为单链表,需遍历所有节点 | |
| 平均时间 | 随机插入情况下,平均查找长度约为 | |
| 空间复杂度 | 递归实现时为 ,迭代实现为 , 为树高 |
3. 二叉搜索树的插入
二叉搜索树的插入:在二叉搜索树中插入一个值为 的节点(假设当前树中不存在 )。
3.1 插入算法步骤
二叉搜索树的插入过程与查找类似,具体如下:
- 如果当前树为空,直接创建值为 的节点,作为根节点返回。
- 如果当前树非空,将 与当前节点 比较:
- 如果 ,递归插入到左子树。
- 如果 ,递归插入到右子树。
注意:二叉搜索树不允许重复节点。如果 已存在于树中,则不插入,直接返回原树。
3.2 插入算法代码实现
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val # 节点值
self.left = left # 左子节点
self.right = right # 右子节点
class Solution:
def insertIntoBST(self, root: TreeNode, val: int) -> TreeNode:
"""
在二叉搜索树中插入一个值为 val 的节点
参数:
root: TreeNode,二叉搜索树的根节点
val: int,待插入的节点值
返回:
TreeNode,插入后的二叉搜索树根节点
"""
if root is None:
# 当前子树为空,直接创建新节点并返回
return TreeNode(val)
if val < root.val:
# 待插入值小于当前节点值,递归插入到左子树
root.left = self.insertIntoBST(root.left, val)
elif val > root.val:
# 待插入值大于当前节点值,递归插入到右子树
root.right = self.insertIntoBST(root.right, val)
# 如果 val == root.val,不插入(不允许重复),直接返回原树
return root4. 二叉搜索树的创建
二叉搜索树的创建:根据给定数组中的元素,依次插入,构建出一棵二叉搜索树。
4.1 创建算法步骤
二叉搜索树的创建通常从一棵空树开始,依次将数组中的每个元素插入到树中,最终形成完整的二叉搜索树。具体步骤如下:
- 初始化根节点为空。
- 遍历数组,将每个元素 依次插入到当前的二叉搜索树中。
- 所有元素插入完成后,返回二叉搜索树的根节点。
4.2 创建代码实现
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val # 节点值
self.left = left # 左子节点
self.right = right # 右子节点
class Solution:
def insertIntoBST(self, root: TreeNode, val: int) -> TreeNode:
"""
在二叉搜索树中插入一个值为 val 的节点
参数:
root: TreeNode,二叉搜索树的根节点
val: int,待插入的节点值
返回:
TreeNode,插入后的二叉搜索树根节点
"""
if root is None:
# 当前子树为空,直接创建新节点并返回
return TreeNode(val)
if val < root.val:
# 待插入值小于当前节点值,递归插入到左子树
root.left = self.insertIntoBST(root.left, val)
elif val > root.val:
# 待插入值大于当前节点值,递归插入到右子树
root.right = self.insertIntoBST(root.right, val)
# 如果 val == root.val,不插入(不允许重复),直接返回原树
return root
def buildBST(self, nums) -> TreeNode:
"""
根据给定数组 nums 创建一棵二叉搜索树
参数:
nums: List[int],待插入的节点值数组
返回:
TreeNode,构建好的二叉搜索树根节点
"""
root = None # 初始化根节点为空
for num in nums:
root = self.insertIntoBST(root, num) # 依次插入每个元素
return root5. 二叉搜索树的删除
二叉搜索树的删除:即在二叉搜索树中删除值为 的节点。
5.1 删除操作算法步骤
在二叉搜索树中删除节点时,首先需要定位到目标节点,然后根据其子树情况分为三种情形:
- 左子树为空:用其右子树替代被删除节点的位置。
- 右子树为空:用其左子树替代被删除节点的位置。
- 左右子树均不为空:利用二叉搜索树的有序性,可用「直接前驱」或「直接后继」节点的值替换当前节点,然后递归删除前驱或后继节点。
- 直接前驱:即左子树中值最大的节点(左子树最右侧节点)。
- 直接后继:即右子树中值最小的节点(右子树最左侧节点)。
具体删除步骤如下:
- 如果当前节点为空,直接返回。
- 如果当前节点值大于 ,递归在左子树中查找并删除,更新 。
- 如果当前节点值小于 ,递归在右子树中查找并删除,更新 。
- 如果当前节点值等于 ,即找到目标节点,分三种情况处理:
- 如果左子树为空,返回右子树(右子树顶替当前节点)。
- 如果右子树为空,返回左子树(左子树顶替当前节点)。
- 如果左右子树均不为空,将左子树整体接到右子树的最左侧节点下,然后返回右子树作为新的子树根节点。
5.2 二叉搜索树的删除代码实现
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def deleteNode(self, root: TreeNode, val: int) -> TreeNode:
"""
在二叉搜索树中删除值为 val 的节点,并返回新的根节点
参数:
root: TreeNode,当前子树的根节点
val: int,待删除的节点值
返回:
TreeNode,删除节点后的新根节点
"""
if not root:
# 递归终止条件:未找到目标节点,直接返回
return None
if val < root.val:
# 待删除值小于当前节点,递归去左子树删除
root.left = self.deleteNode(root.left, val)
return root
elif val > root.val:
# 待删除值大于当前节点,递归去右子树删除
root.right = self.deleteNode(root.right, val)
return root
else:
# 找到目标节点,分三种情况处理
if not root.left:
# 情况 1:左子树为空,直接返回右子树
return root.right
elif not root.right:
# 情况 2:右子树为空,直接返回左子树
return root.left
else:
# 情况 3:左右子树均不为空
# 找到右子树的最左节点(即后继节点)
successor = root.right
while successor.left:
successor = successor.left
# 用后继节点的值替换当前节点
root.val = successor.val
# 在右子树中递归删除后继节点
root.right = self.deleteNode(root.right, successor.val)
return root6. 总结
6.1 核心特性
二叉搜索树(BST)是一种 有序的二叉树结构,其核心特性是:
- 左子树所有节点值 < 根节点值 < 右子树所有节点值
- 中序遍历结果是有序的(递增序列)
- 每个节点的左右子树也都是二叉搜索树
6.2 基本操作算法分析
| 操作 | 最优时间 | 最坏时间 | 平均时间 | 空间复杂度 |
|---|---|---|---|---|
| 查找 | O(log n) | O(n) | O(log n) | O(1) |
| 插入 | O(log n) | O(n) | O(log n) | O(1) |
| 删除 | O(log n) | O(n) | O(log n) | O(1) |
说明:最优情况是树接近完全平衡,最坏情况是树退化为单链表。
6.3 算法特点
- 优点:
- 查找、插入、删除效率高(平均 O(log n))
- 支持范围查询和有序遍历
- 实现相对简单,易于理解
- 缺点:
- 插入顺序影响树的高度和性能
- 不平衡时可能退化为链表( 复杂度)
- 需要额外的平衡机制(如 AVL 树、红黑树)
练习题目
参考资料
- 【书籍】算法训练营 陈小玉 著
- 【书籍】算法竞赛入门经典:训练指南 - 刘汝佳,陈锋 著
- 【书籍】算法竞赛进阶指南 - 李煜东 著
- 【博文】7.4 二叉搜索树 - Hello 算法