6.1 图的定义和分类

---

1. 图的定义

图（Graph）：由顶点集合 $V$ 和边集合 $E$（即顶点之间的连接关系）组成的数据结构，通常记作 $G = (V, E)$。

• 顶点（Vertex）：图的基本单元，表示对象或节点。顶点集合 $V$ 是有限且非空的，包含 $n > 0$ 个顶点。通常用圆圈表示顶点。
• 边（Edge）：连接两个顶点的线段，表示它们之间的关系。边可记为 $e = \langle u, v \rangle$，表示从 $u$ 到 $v$ 的一条边，其中 $u$ 是起点，$v$ 是终点。

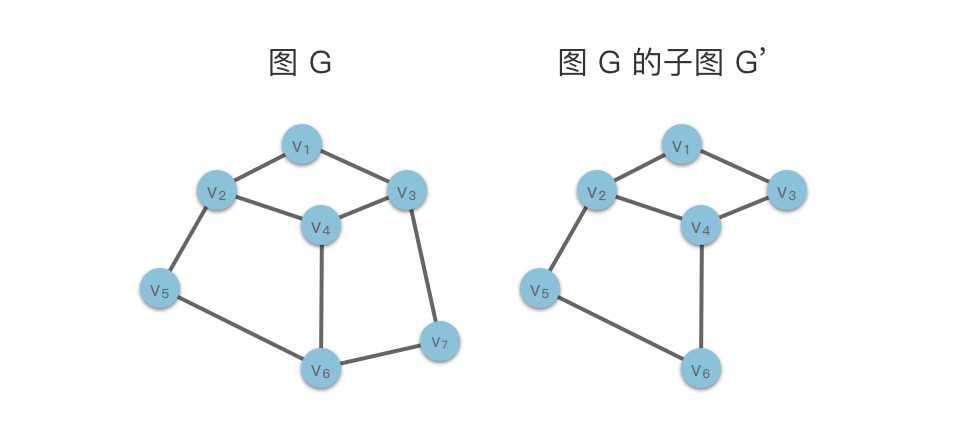
• 子图（Sub Graph）：如果图 $G' = (V', E')$ 满足 $V' \subseteq V$ 且 $E' \subseteq E$，则 $G'$ 是 $G$ 的子图。也就是说，子图由原图部分顶点和边组成，且边的两个端点都属于 $V'$。特别地，$G$ 本身也是它的一个子图。下图展示了图 $G$ 及其子图 $G'$。

2. 图的分类

2.1 无向图与有向图

按边是否有方向，可以将图分为「无向图」和「有向图」。

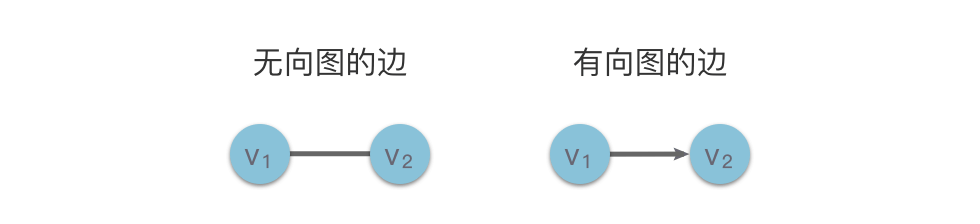
• 无向图（Undirected Graph）：边没有方向，常用于表示朋友关系、城市间双向道路等。无向图的边由两个顶点组成的无序对表示，如下图左侧中的顶点 $(v_1, v_2)$。

• 有向图（Directed Graph）：边有方向，常用于表示任务流程、依赖关系等。有向图的边（弧）由两个顶点组成的有序对表示，如下图右侧中的顶点 $\langle v_1, v_2 \rangle$，其中 $v_1$ 为弧尾，$v_2$ 为弧头。

如果图有 $n$ 个顶点，则：

• 无向图最大边数：$\frac{n \times (n - 1)}{2}$。达到最大边数的无向图称为 完全无向图。
• 有向图最大边数：$n \times (n - 1)$。达到最大边数的有向图称为 完全有向图。

下图左为 $4$ 个顶点的完全无向图，右为 $4$ 个顶点的完全有向图：

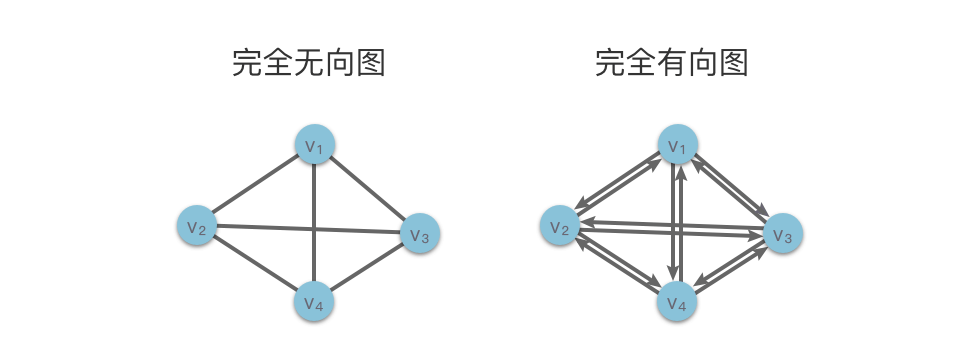
顶点的度 是图的一个重要概念：

• 无向图中，顶点的度：与该顶点相连的边的数量，记为 $TD(v_i)$。
  • 如上图左，$v_3$ 的度为 $3$。
• 有向图中，顶点的度 分为：
  • 出度（Out Degree）：以该顶点为起点的边数，记为 $OD(v_i)$。
  • 入度（In Degree）：以该顶点为终点的边数，记为 $ID(v_i)$。
  • 顶点总度：$TD(v_i) = OD(v_i) + ID(v_i)$。
  • 如上图右，$v_3$ 的出度为 $3$，入度为 $3$，总度为 $6$。

2.2 环形图和无环图

路径：路径是图论中的核心概念。对于图 $G = (V, E)$，如果存在顶点序列 $v_{i_0}, v_{i_1}, v_{i_2}, \ldots, v_{i_m}$，使得任意相邻顶点对之间都存在边相连（无向图为 $(v_{i_{k-1}}, v_{i_k}) \in E$，有向图为 $\langle v_{i_{k-1}}, v_{i_k} \rangle \in E$，$1 \leq k \leq m$），则称该顶点序列为从 $v_{i_0}$ 到 $v_{i_m}$ 的一条路径。其中，$v_{i_0}$ 为起点，$v_{i_m}$ 为终点。

简而言之，如果从顶点 $v_{i_0}$ 出发，经过若干顶点和边能够到达顶点 $v_{i_m}$，则称 $v_{i_0}$ 与 $v_{i_m}$ 之间存在一条路径，所经过的顶点序列即为这条路径。

• 环（Cycle）：如果一条路径的起点和终点重合（即 $v_{i_0} = v_{i_m}$），则称该路径为「环」或「回路」。
• 简单路径：路径上所有顶点均不重复出现（除非是环的首尾重合），称为「简单路径」。

根据图中是否存在环，可以将图分为「环形图」和「无环图」：

• 环形图（Cyclic Graph）：如果图中至少存在一条环（Cycle），则称该图为环形图或含环图。
• 无环图（Acyclic Graph）：如果图中不存在任何环，则称该图为无环图。

对于有向图，如果不存在环，则称为「有向无环图（Directed Acyclic Graph, DAG）」。DAG 结构在动态规划、最短路径、数据压缩等算法中有着广泛应用。

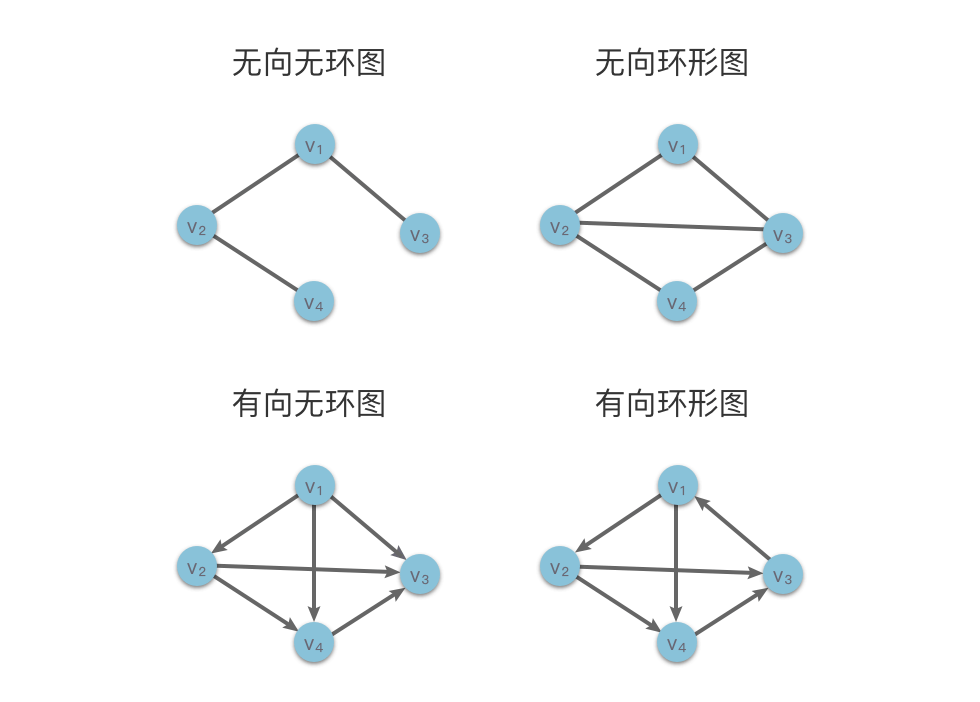
下图展示了四类典型图结构：无向无环图、无向环形图、有向无环图和有向环形图。其中有向环形图中，顶点 $v_1$、$v_2$、$v_3$ 及其相连的边构成了一个环。

环形图和无环图

2.3 连通图与非连通图

2.3.1 连通无向图

在无向图中，如果从顶点 $v_i$ 能通过一条路径到达顶点 $v_j$，则称 $v_i$ 和 $v_j$ 连通。

• 连通无向图：任意两个顶点之间都有路径相连的无向图。
• 非连通无向图：存在至少一对顶点之间没有路径相连的无向图。

下图左侧为连通无向图，$v_1$ 能与所有其他顶点连通；右侧为非连通无向图，$v_1$ 只能与 $v_2$、$v_3$、$v_4$ 连通，无法到达 $v_5$、$v_6$。

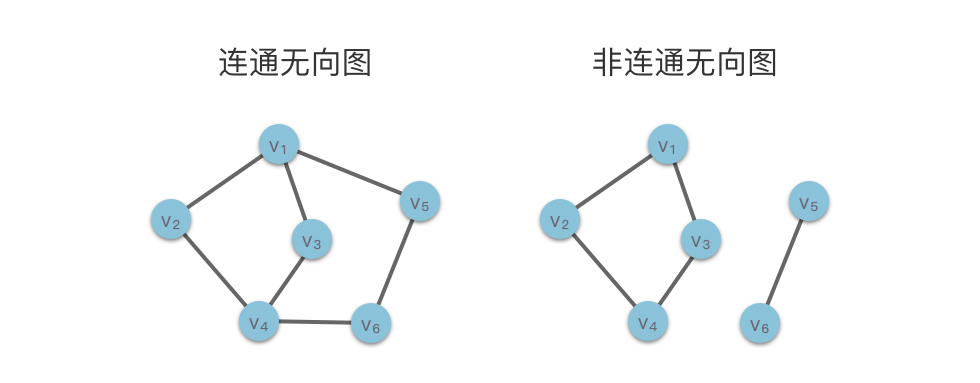
2.3.2 无向图的连通分量

在无向图中，整体可能不是连通的，但其中的某些子图是连通的，这些子图称为「连通子图」。如果一个连通子图无法再被包含于更大的连通子图中，则称其为「连通分量」，即无向图中的极大连通子图。

• 连通子图：无向图的一个子图，且该子图是连通的。
• 极大连通子图：连通子图中，如果不存在包含它的更大的连通子图，则称为极大连通子图。
• 连通分量：无向图中的极大连通子图，即为该图的连通分量。

举例来说，上图右侧的非连通无向图中，顶点 $v_1$、$v_2$、$v_3$、$v_4$ 及其相连的边构成了一个连通子图，且无法再扩展为更大的连通子图，因此它是原图的一个连通分量。同理，顶点 $v_5$、$v_6$ 及其相连的边也构成了另一个连通分量。

2.3.3 强连通有向图

在有向图中，如果顶点 $v_i$ 能到达 $v_j$，且 $v_j$ 也能到达 $v_i$，则称 $v_i$ 和 $v_j$ 是「强连通」的。

• 强连通有向图：任意两个顶点都能互相到达的有向图。
• 非强连通有向图：存在至少一对顶点不能互相到达的有向图。

下图左为强连通有向图，任意两点可互达；右图中 $v_7$ 无法到达其他顶点，因此不是强连通有向图。

2.3.4 有向图的强连通分量

在有向图中，「强连通分量」指的是：图中某个极大子图，子图内任意两个顶点都可以互相到达（即强连通），并且无法再加入其他顶点使其仍然强连通。

简要定义如下：

• 强连通子图：有向图的一个子图，子图内任意两点互相可达。
• 极大强连通子图：不能再加入其他顶点的强连通子图。
• 强连通分量：有向图中的极大强连通子图。

举例说明：上图右侧的有向图不是强连通图（如 $v_7$ 无法到达其他顶点），但 $v_1$、$v_2$、
$v_3$、$v_4$、$v_5$、$v_6$ 及其边构成了一个强连通分量（即左侧图）。而 $v_7$ 自身也单独构成一个强连通分量。

2.4 带权图

有些图不仅表示顶点之间是否有关系，还需要描述这种关系的「强度」或「代价」，这就是「权」。权值可以表示距离、时间、费用等。

• 带权图：每条边都带有权值的图。权值一般为非负数，有时也可以为负数。
• 网络：带权且连通的无向图称为网络。

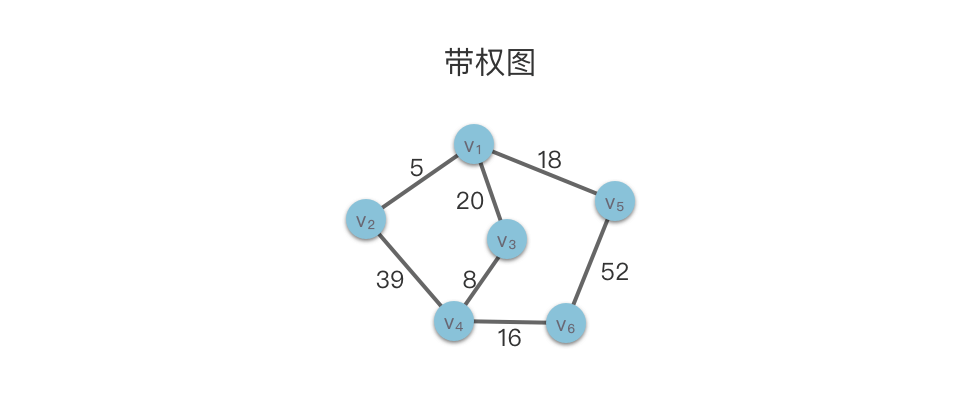
下图展示了一个带权图的例子：

2.5 稠密图与稀疏图

图按边的多少可分为「稠密图」和「稀疏图」，这一划分没有严格的界限，仅为便于理解。

• 稠密图（Dense Graph）：边数接近完全图的图，即大多数顶点之间都有边相连。
• 稀疏图（Sparse Graph）：边数远少于完全图的图（常见如 $e < n \times \log_2 n$），大部分顶点之间没有直接连接。

3. 总结

图是计算机科学中最重要的数据结构之一，由顶点和边组成，用于表示对象间的关系。本文介绍了图的基本概念和分类：

核心概念

• 顶点（Vertex）：图的基本单元，表示对象或节点
• 边（Edge）：连接顶点的线段，表示对象间的关系
• 路径：顶点序列，表示从一个顶点到另一个顶点的遍历过程

主要分类

1. 按方向性：无向图（双向关系）vs 有向图（单向关系）
2. 按连通性：连通图（任意两点可达）vs 非连通图（存在孤立部分）
3. 按环结构：环形图（存在回路）vs 无环图（无回路，如DAG）
4. 按权值：带权图（边有权重）vs 无权图（边无权重）
5. 按密度：稠密图（边多）vs 稀疏图（边少）

重要特性

• 度：无向图中顶点的连接数，有向图中分为入度和出度
• 连通分量：无向图中的极大连通子图
• 强连通分量：有向图中任意两点互相可达的极大子图

理解这些基础概念是学习图算法（如 DFS、BFS、最短路径、最小生成树等）的重要前提。

参考资料

• 【书籍】ACM-ICPC 程序设计系列 - 图论及应用 - 陈宇 吴昊 主编
• 【书籍】数据结构教程 第 3 版 - 唐发根 著
• 【书籍】大话数据结构 - 程杰 著
• 【书籍】算法训练营 - 陈小玉 著
• 【书籍】Python 数据结构与算法分析 第 2 版 - 布拉德利·米勒 戴维·拉努姆 著
• 【博文】图的基础知识 | 小浩算法
• 【博文】链式前向星及其简单应用 | Malash's Blog