6.2 图的存储结构和问题应用

ITCharge大约 19 分钟

6.2 图的存储结构和问题应用

---

1. 图的存储结构

图是一种由顶点和边构成的复杂数据结构，通常包含若干（有限个）顶点，任意两个顶点之间都可能通过边相连。在实现图的存储时，关键在于如何高效地表示顶点与边之间的关系。

常见的图存储方式主要分为「顺序存储结构」和「链式存储结构」两大类。顺序存储结构包括邻接矩阵和边集数组；链式存储结构则有邻接表、链式前向星、十字链表、邻接多重表等。

下面将详细介绍几种常用的图存储结构。文中约定： $n$ 表示顶点数， $m$ 表示边数， $TD(v_i)$ 表示顶点 $v_i$ 的度数。

1.1 邻接矩阵

1.1.1 邻接矩阵的原理描述

邻接矩阵（Adjacency Matrix）：通过一个二维数组 $adj$ 来表示顶点之间的连接关系。
对于无权图，如果 $adj[i][j] == 1$ ，表示顶点 $v_i$ 与 $v_j$ 之间有边；如果 $adj[i][j] = 0$ ，则表示两者之间无边。
对于带权图，如果 $adj[i][j] == w$ 且 $w \ne \infty$ ，则表示 $v_i$ 到 $v_j$ 有一条权值为 $w$ 的边；如果 $adj[i][j] = \infty$ ，则表示两者之间无边。

下图左侧为一个无向图，右侧为其对应的邻接矩阵结构示意：

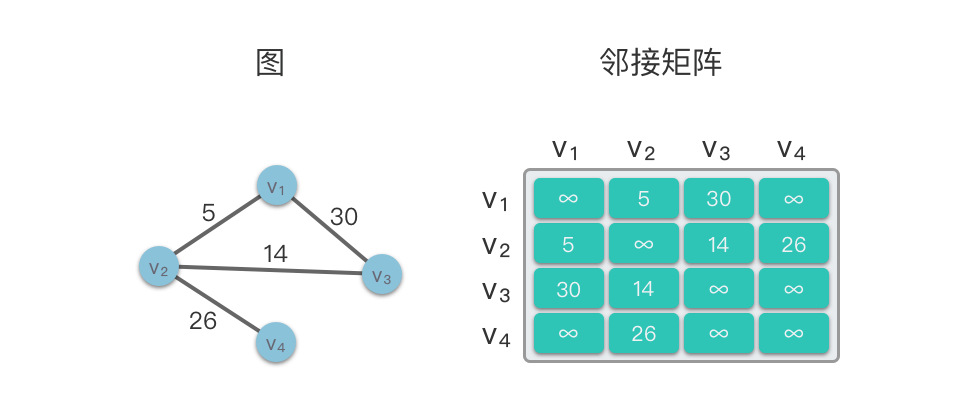
邻接矩阵的主要特点如下：

优点：结构简单，便于实现；可以快速判断任意两个顶点之间是否存在边，也能直接获取边的权值。
缺点：初始化和遍历效率较低，空间占用大且利用率不高，无法表示重边，顶点的增删操作不便。当顶点数量较大（如 $n > 10^5$ ）时，采用空间复杂度为 $n \times n$ 的二维数组存储邻接矩阵在实际应用中难以实现。

1.1.2 邻接矩阵的代码实现

class Graph:                                       # 邻接矩阵实现的图
    def __init__(self, ver_count, directed=False, inf=float('inf')):
        self.n = ver_count                         # 顶点数量 n
        self.directed = directed                   # 是否为有向图
        self.inf = inf                             # 无边时的填充值（带权图用 ∞ 表示无边）
        # 邻接矩阵，采用 1..n 顶点编号；0 号行列弃用，便于直观
        self.adj = [[inf] * (ver_count + 1) for _ in range(ver_count + 1)]
        for i in range(1, ver_count + 1):
            self.adj[i][i] = 0                    # 自环距离为 0（无权图也可视作 0）

    def add_edge(self, vi, vj, w=1):               # 添加边 vi -> vj，权重默认为 1
        self.adj[vi][vj] = w
        if not self.directed:                      # 无向图需要对称赋值
            self.adj[vj][vi] = w

    def get_edge(self, vi, vj):                    # 查询边权，不存在返回 None
        if self.adj[vi][vj] != self.inf:
            return self.adj[vi][vj]
        return None

    def printMatrix(self):                         # 打印邻接矩阵，∞ 表示无边
        for i in range(1, self.n + 1):
            row = [self.adj[i][j] if self.adj[i][j] != self.inf else '∞' for j in range(1, self.n + 1)]
            print(' '.join(map(str, row)))


# 示例：构建一个有向带权图，并进行查询与打印
graph = Graph(6, directed=True)
edges = [(1, 2, 5), (1, 5, 6), (2, 4, 7), (4, 3, 9), (3, 1, 2), (5, 6, 8), (6, 4, 3)]
for u, v, w in edges:
    graph.add_edge(u, v, w)

print(graph.get_edge(4, 3))   # 输出 9（存在边 4->3，权重 9）
print(graph.get_edge(4, 5))   # 输出 None（不存在边 4->5）
graph.printMatrix()           # 打印 6x6 邻接矩阵

1.1.3 邻接矩阵的算法分析

时间复杂度：
- 初始化： $O(n^2)$ 。需要为 $n$ 个顶点分配 $n \times n$ 的二维数组空间。
- 查询、添加或删除一条边： $O(1)$ 。通过下标即可直接访问和修改边的信息。
- 获取某个顶点的所有邻接边： $O(n)$ 。需遍历该顶点所在的整行或整列。
- 遍历整张图： $O(n^2)$ 。需要访问整个邻接矩阵。
空间复杂度： $O(n^2)$ 。无论实际边数多少，均需分配 $n \times n$ 的空间。

1.2 邻接表

1.2.1 邻接表的原理描述

邻接表（Adjacency List）：一种结合顺序存储与链式存储的图结构。它主要由两部分组成：一是用于存放所有顶点信息的数组，二是用于存放每个顶点所有邻接边的链表。

在邻接表中，每个顶点 $v_i$ 都对应一个链表，链表中的每个节点表示一条从 $v_i$ 出发的边，节点中存储该边所指向的顶点及相关信息。因此，如果图有 $n$ 个顶点，则邻接表由 $n$ 个链表组成，每个链表分别记录对应顶点的所有邻接边。

每个顶点在邻接表中都有一个表头节点（即「顶点节点」），该节点包含顶点本身的信息和指向其第一条邻接边的指针。这样可以高效地访问和管理每个顶点的所有邻接边。

为了便于随机访问任意顶点的邻接链表，通常将所有顶点节点以数组形式顺序存储，数组下标即为顶点在图中的编号。

下图左侧为一个有向图，右侧为其对应的邻接表结构示意：

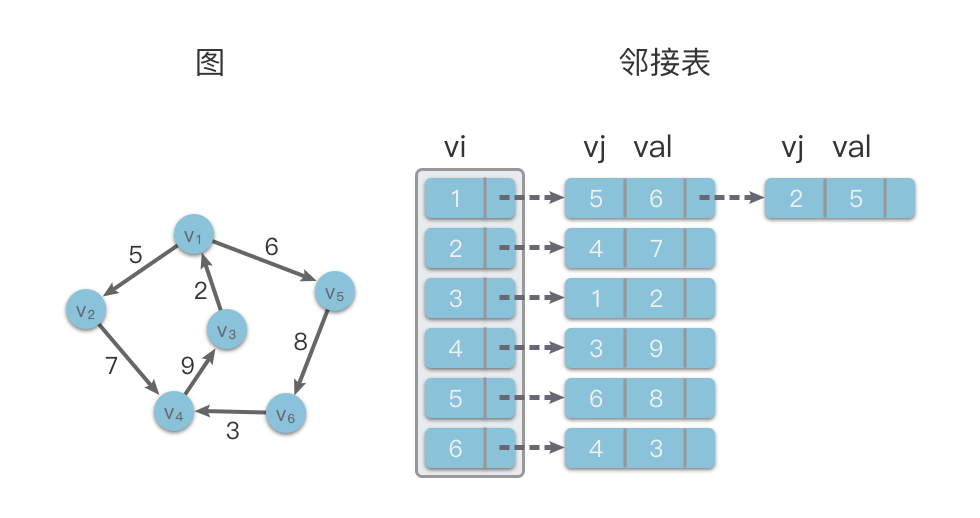
1.2.2 邻接表的代码实现

class EdgeNode:                                 # 边结点：存储终点、权值与下一条边
    def __init__(self, vj, val):
        self.vj = vj                            # 边的终点
        self.val = val                          # 边的权值（无权图可默认 1）
        self.next = None                        # 指向下一条同起点的边

class VertexNode:                               # 顶点结点：存储顶点编号与其第一条邻接边
    def __init__(self, vi):
        self.vi = vi                            # 顶点编号
        self.head = None                        # 指向该顶点的第一条邻接边

class Graph:                                    # 邻接表实现的图
    def __init__(self, ver_count, directed=False):
        self.n = ver_count                      # 顶点数量 n
        self.directed = directed                # 是否为有向图
        # 使用 1..n 的顶点编号，0 号位置空置，便于直观
        self.vertices = [None] + [VertexNode(i) for i in range(1, ver_count + 1)]

    def _valid(self, v):                        # 顶点合法性检查
        return 1 <= v <= self.n

    def add_edge(self, vi, vj, val=1):          # 添加边 vi -> vj，权重默认 1
        if not self._valid(vi) or not self._valid(vj):
            raise ValueError("invalid vertex: {} or {}".format(vi, vj))
        edge = EdgeNode(vj, val)                # 头插法加入邻接链表
        edge.next = self.vertices[vi].head
        self.vertices[vi].head = edge
        if not self.directed:                   # 无向图需要加反向边
            rev = EdgeNode(vi, val)
            rev.next = self.vertices[vj].head
            self.vertices[vj].head = rev

    def get_edge(self, vi, vj):                 # 查询 vi -> vj 的边权，如果无边返回 None
        if not self._valid(vi) or not self._valid(vj):
            raise ValueError("invalid vertex: {} or {}".format(vi, vj))
        cur = self.vertices[vi].head
        while cur:
            if cur.vj == vj:
                return cur.val
            cur = cur.next
        return None

    def neighbors(self, vi):                    # 遍历顶点 vi 的所有邻接边 (vj, val)
        cur = self.vertices[vi].head
        while cur:
            yield cur.vj, cur.val
            cur = cur.next

    def printGraph(self):                       # 打印所有边
        for vi in range(1, self.n + 1):
            cur = self.vertices[vi].head
            while cur:
                print(str(vi) + ' - ' + str(cur.vj) + ' : ' + str(cur.val))
                cur = cur.next


# 示例：构建有向带权图并查询/打印
graph = Graph(6, directed=True)
edges = [(1, 2, 5), (1, 5, 6), (2, 4, 7), (4, 3, 9), (3, 1, 2), (5, 6, 8), (6, 4, 3)]
for u, v, w in edges:
    graph.add_edge(u, v, w)

print(graph.get_edge(4, 3))   # 9
print(graph.get_edge(4, 5))   # None（无此边）
graph.printGraph()

1.2.3 邻接表的算法分析

时间复杂度分析：
- 图的初始化与创建： $O(n + m)$ ，其中 $n$ 表示顶点数， $m$ 表示边数。因为需要为每个顶点分配空间，并依次插入每条边。
- 查询是否存在 $v_i$ 到 $v_j$ 的边： $O(TD(v_i))$ ，其中 $TD(v_i)$ 表示顶点 $v_i$ 的出度。由于邻接表只存储与 $v_i$ 直接相连的边，因此需要遍历 $v_i$ 的所有邻接点，最坏情况下需遍历 $v_i$ 的全部出边。
- 遍历某个顶点的所有边： $O(TD(v_i))$ ，即与该顶点相连的所有边都需访问一遍，效率较高。
- 遍历整张图的所有边： $O(n + m)$ 。遍历所有顶点，每个顶点的邻接表总共包含 $m$ 条边，因此整体遍历代价为 $O(n + m)$ 。
空间复杂度分析： $O(n + m)$ ，邻接表需要为每个顶点分配一个链表头结点（ $O(n)$ ），并为每条边分配一个边节点（ $O(m)$ ），因此总空间复杂度为 $O(n + m)$ 。相比邻接矩阵，邻接表在稀疏图中能显著节省空间。

1.3 链式前向星

1.3.1 链式前向星的原理描述

链式前向星（Linked Forward Star），又称静态邻接表，是一种以静态链表实现邻接表的高效图存储结构。它将边集数组与邻接表结合，能够高效地访问某个节点的所有邻接点，并且空间开销极小。

链式前向星采用静态链表的方式存储边信息，是目前建图和遍历效率极高的存储方法之一。

其核心由两类数据结构组成：

边集数组 $edges$ ： $edges[i]$ 表示第 $i$ 条边，包含以下信息： $edges[i].vj$ 为该边的终点， $edges[i].val$ 为该边的权值， $edges[i].next$ 指向与该边起点相同的下一条边在 $edges$ 数组中的下标。
头节点数组 $head$ ： $head[i]$ 存储以顶点 $i$ 为起点的第一条边在 $edges$ 数组中的下标。

链式前向星的核心思想是通过 $head$ 数组记录每个顶点的第一条出边在 $edges$ 数组中的下标，并利用 $edges$ 数组中每条边的 $next$ 字段，将同一起点的所有出边以静态链表的形式串联起来，从而高效地关联顶点 $v_i$ 及其所有出边。

如下图所示，左侧为一个有向图，右侧为其对应的链式前向星结构。

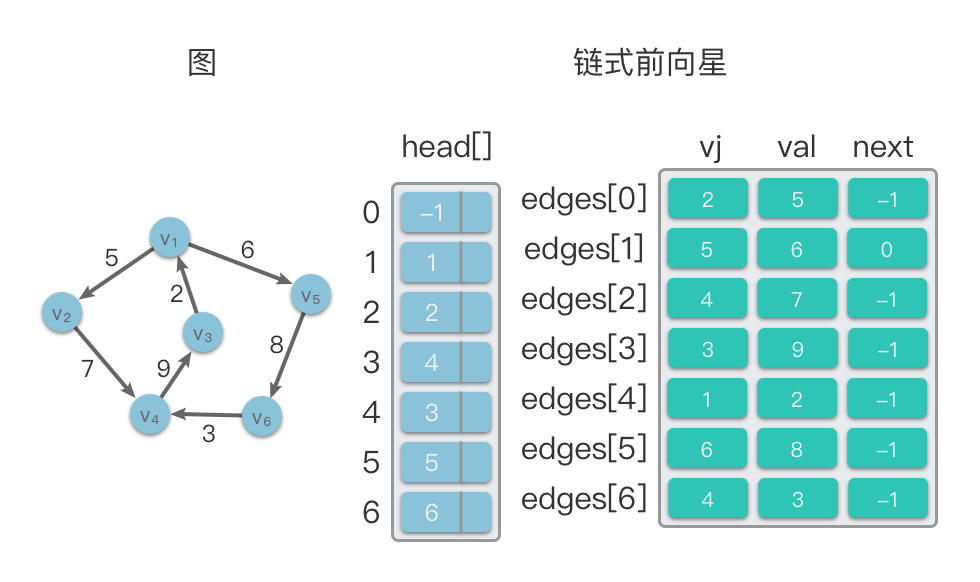
以遍历顶点 $v_1$ 的所有出边为例，步骤如下：

首先，通过 index = head[1] = 1，找到以 $v_1$ 为起点的第一条边在 edges 数组中的下标，即 edges[1]，对应边 $\langle v_1, v_5 \rangle$ ，权值为 6。
然后，根据 index = edges[1].next = 0，找到第二条边 edges[0]，即 $\langle v_1, v_2 \rangle$ ，权值为 5。
最后，index = edges[0].next = -1，表示没有更多的出边，遍历结束。

1.3.2 链式前向星的代码实现

class EdgeNode:
    """边信息类，存储终点、权值和下一条边的下标"""
    def __init__(self, vj, val, next_idx):
        self.vj = vj        # 边的终点
        self.val = val      # 边的权值
        self.next = next_idx  # 下一条边在边集数组中的下标

class Graph:
    """链式前向星图结构"""
    def __init__(self, ver_count):
        self.n = ver_count          # 顶点个数
        self.head = [-1] * self.n   # 头节点数组，head[i]为顶点i的第一条出边下标
        self.edges = []             # 边集数组

    def _valid(self, v):
        """判断顶点编号是否合法（0 ~ n - 1）"""
        return 0 <= v < self.n

    def add_edge(self, vi, vj, val):
        """
        添加一条边 vi -> vj，权值为 val
        vi, vj 均为 0 ~ n - 1 的顶点编号
        """
        if not self._valid(vi) or not self._valid(vj):
            raise ValueError(f"{vi} 或 {vj} 不是有效顶点编号")
        # 新边的 next 指向 vi 原来的第一条出边
        edge = EdgeNode(vj, val, self.head[vi])
        self.edges.append(edge)
        self.head[vi] = len(self.edges) - 1  # head[vi] 指向新加边的下标

    def build(self, edge_list):
        """批量建图，edge_list 为 [(vi, vj, val), ...]，顶点编号从 1 开始"""
        for vi, vj, val in edge_list:
            # 由于输入的顶点编号是从 1 开始，内部实现是从 0 开始，所以需要减 1
            self.add_edge(vi - 1, vj - 1, val)  

    def get_edge(self, vi, vj):
        """
        查询 vi -> vj的边权，vi, vj 为 1-based 编号
        返回权值或 None
        """
        vi -= 1
        vj -= 1
        if not self._valid(vi) or not self._valid(vj):
            raise ValueError(f"{vi + 1} 或 {vj + 1} 不是有效顶点编号")
        idx = self.head[vi]
        while idx != -1:
            edge = self.edges[idx]
            if edge.vj == vj:
                return edge.val
            idx = edge.next
        return None

    def printGraph(self):
        """打印所有边，顶点编号输出为 1-based"""
        for vi in range(self.n):
            idx = self.head[vi]
            while idx != -1:
                edge = self.edges[idx]
                print(f"{vi+1} - {edge.vj+1} : {edge.val}")
                idx = edge.next

# 示例：构建有向带权图并查询 / 打印
graph = Graph(7)  # 顶点编号 1 ~ 7
edges = [
    [1, 2, 5], [1, 5, 6], [2, 4, 7],
    [4, 3, 9], [3, 1, 2], [5, 6, 8], [6, 4, 3]
]
graph.build(edges)
print(graph.get_edge(4, 3))   # 输出 9
print(graph.get_edge(4, 5))   # 输出 None（无此边）
graph.printGraph()

1.3.3 链式前向星的算法分析

时间复杂度：
- 图的初始化和创建操作： $O(n + m)$ ，其中 $n$ 表示顶点数， $m$ 表示边数。初始化时需要为每个顶点分配空间，并依次插入每条边，因此总耗时与顶点和边的数量成线性关系。
- 查询是否存在 $v_i$ 到 $v_j$ 的边： $O(TD(v_i))$ ，其中 $TD(v_i)$ 表示顶点 $v_i$ 的出度。因为链式前向星存储结构需要遍历 $v_i$ 的所有出边才能判断是否存在到 $v_j$ 的边，最坏情况下需要遍历 $v_i$ 的所有出边。
- 遍历某个点的所有边： $O(TD(v_i))$ 。由于每个顶点的出边在链表中连续存储，遍历时只需顺序访问即可，效率较高。
- 遍历整张图的所有边： $O(n + m)$ 。遍历所有顶点并依次访问每个顶点的所有出边，总共访问 $n$ 个顶点和 $m$ 条边，整体复杂度为线性。
空间复杂度： $O(n + m)$ 。需要为每个顶点分配一个头指针（ $O(n)$ ），并为每条边分配一个边节点（ $O(m)$ ），因此总空间消耗与顶点数和边数之和成正比。

1.4 哈希表实现邻接表

1.4.1 哈希表实现邻接表的原理描述

在 Python 中，可以利用哈希表（即字典）高效地实现邻接表结构。具体做法是：使用一个字典存储所有顶点信息，字典的键为顶点编号，值为该顶点的邻接边集合（同样用一个字典表示）。每个顶点对应的邻接边字典，其键为相邻顶点的编号，值为对应边的权重。这样既方便查询某一顶点的所有出边，也便于获取任意一条边的权重。

1.4.2 哈希表实现邻接表的代码实现

class Graph:
    """哈希表实现的邻接表图结构"""
    def __init__(self, ver_count, directed=False):
        self.n = ver_count                    # 顶点数量
        self.directed = directed              # 是否为有向图
        # 使用字典存储邻接表，键为顶点编号，值为邻接边字典
        # 邻接边字典：键为相邻顶点编号，值为边权重
        self.adj = {i: {} for i in range(1, ver_count + 1)}

    def _valid(self, v):
        """判断顶点编号是否合法（1 ~ n）"""
        return 1 <= v <= self.n

    def add_edge(self, vi, vj, val=1):
        """
        添加一条边 vi -> vj，权值为 val
        vi, vj 为 1-based 顶点编号
        """
        if not self._valid(vi) or not self._valid(vj):
            raise ValueError(f"顶点编号 {vi} 或 {vj} 超出范围 [1, {self.n}]")
        
        # 添加边 vi -> vj
        self.adj[vi][vj] = val
        
        # 如果是无向图，添加反向边
        if not self.directed:
            self.adj[vj][vi] = val

    def build(self, edge_list):
        """
        批量建图
        edge_list: [(vi, vj, val), ...] 边列表，顶点编号从1开始
        """
        for vi, vj, val in edge_list:
            self.add_edge(vi, vj, val)

    def get_edge(self, vi, vj):
        """
        查询 vi -> vj 的边权
        返回权值，如果不存在该边则返回 None
        """
        if not self._valid(vi) or not self._valid(vj):
            raise ValueError(f"顶点编号 {vi} 或 {vj} 超出范围 [1, {self.n}]")
        
        return self.adj[vi].get(vj, None)

    def has_edge(self, vi, vj):
        """
        判断是否存在 vi -> vj 的边
        返回 True 或 False
        """
        if not self._valid(vi) or not self._valid(vj):
            return False
        return vj in self.adj[vi]

    def neighbors(self, vi):
        """
        遍历顶点 vi 的所有邻接边
        返回生成器，每次产生 (邻接顶点, 边权)
        """
        if not self._valid(vi):
            raise ValueError(f"顶点编号 {vi} 超出范围 [1, {self.n}]")
        
        for vj, val in self.adj[vi].items():
            yield vj, val

    def get_degree(self, vi):
        """
        获取顶点 vi 的出度
        """
        if not self._valid(vi):
            raise ValueError(f"顶点编号 {vi} 超出范围 [1, {self.n}]")
        return len(self.adj[vi])

    def print_graph(self):
        """打印所有边"""
        for vi in range(1, self.n + 1):
            for vj, val in self.adj[vi].items():
                print(f"{vi} -> {vj} : {val}")


# 示例：构建有向带权图并测试各种操作

# 创建有向图
graph = Graph(6, directed=True)

# 添加边
edges = [(1, 2, 5), (1, 5, 6), (2, 4, 7), (4, 3, 9), (3, 1, 2), (5, 6, 8), (6, 4, 3)]
graph.build(edges)

print("=== 图的基本信息 ===")
print(f"顶点数: {graph.n}")
print(f"是否为有向图: {graph.directed}")

print("\n=== 边的查询操作 ===")
print(f"边 4->3 的权重: {graph.get_edge(4, 3)}")  # 输出: 9
print(f"边 4->5 的权重: {graph.get_edge(4, 5)}")  # 输出: None
print(f"是否存在边 1->2: {graph.has_edge(1, 2)}")  # 输出: True
print(f"是否存在边 2->1: {graph.has_edge(2, 1)}")  # 输出: False

print("\n=== 邻接点遍历 ===")
for vi in range(1, 7):
    neighbors = list(graph.neighbors(vi))
    print(f"顶点 {vi} 的邻接点: {neighbors}, 出度: {graph.get_degree(vi)}")

print("\n=== 所有边 ===")
graph.print_graph()

1.4.3 哈希表实现邻接表的简单构建

在实际刷题或竞赛过程中，如果只是需要临时构建一张图用于算法实现，通常会采用最简单直接的方式来初始化邻接表。例如，直接用 Python 的字典（dict）或列表（list）来存储邻接关系，无需封装成类，也不必实现完整的接口。这样可以大大简化代码量，便于快速调试和提交。

# 构建图
n = 6  # 顶点数
edges = [(1, 2, 5), (1, 5, 6), (2, 4, 7), (4, 3, 9), (3, 1, 2), (5, 6, 8), (6, 4, 3)]

# 初始化邻接表
graph = {i: {} for i in range(1, n + 1)}

# 添加边
for vi, vj, val in edges:
    graph[vi][vj] = val

# 查询边
print(graph[4].get(3, None))  # 输出: 9
print(graph[4].get(5, None))  # 输出: None

# 遍历邻接点
for vi in range(1, n + 1):
    print(f"顶点 {vi} 的邻接点: {list(graph[vi].keys())}")

1.4.4 哈希表实现邻接表的算法分析

时间复杂度：
- 图的初始化与构建： $O(n + m)$ ，其中 $n$ 表示顶点数， $m$ 表示边数。每个顶点的邻接表初始化为 $O(n)$ ，每条边的插入操作为 $O(1)$ ，总共 $m$ 条边，因此整体为 $O(n + m)$ 。
- 边的存在性查询： $O(1)$ 。判断是否存在从 $v_i$ 到 $v_j$ 的边，利用哈希表查找，平均时间复杂度为 $O(1)$ ，即常数时间即可完成。
- 遍历某一顶点的所有邻接边：遍历顶点 $v_i$ 的所有出边，时间复杂度为 $O(\mathrm{TD}(v_i))$ ，其中 $\mathrm{TD}(v_i)$ 表示顶点 $v_i$ 的出度（即邻接点个数）。这是因为只需顺序访问该顶点邻接表中的所有元素。
- 遍历整张图的所有边：遍历所有顶点及其邻接表，整体时间复杂度为 $O(n + m)$ 。 $O(n)$ 用于访问所有顶点， $O(m)$ 用于访问所有边。
空间复杂度： $O(n + m)$ ，其中 $O(n)$ 用于存储所有顶点的邻接表结构， $O(m)$ 用于存储所有边的信息。相比邻接矩阵，邻接表在稀疏图（ $m \ll n^2$ ）时能显著节省空间。

2. 常见图论问题

常见的图论问题主要有：遍历问题、连通性问题、生成树问题、最短路径问题、网络流问题、二分图问题 等。

2.1 图的遍历问题

图的遍历：从某个顶点出发，按照特定顺序访问图中所有节点且仅访问一次。

遍历是解决连通性、拓扑排序、关键路径等问题的基础。常用方法有：

深度优先搜索（DFS）：沿一条路径尽可能深入，无法继续时回退。
广度优先搜索（BFS）：一层一层访问邻接点，逐层推进。

2.2 图的连通性问题

无向图常见连通性问题有：连通分量、点双连通分量（割点）、边双连通分量（桥）、全局最小割等。

连通分量：无向图中，每个连通分量是内部任意两点都连通、且无法再扩展的极大子图。常用并查集或 DFS/BFS 求解。
点双连通分量（割点）：无向图中，去掉任意一个顶点后，分量内其他顶点仍连通的极大子图。割点是指删除后会增加连通分量数的顶点。常用 DFS 求解。
边双连通分量（桥）：无向图中，去掉任意一条边后，分量内其他顶点仍连通的极大子图。桥是指删除后会增加连通分量数的边。也可用 DFS 求解。
全局最小割：将无向图顶点分为两个不相交集合，使连接这两个集合的边权和最小。常用于网络可靠性分析，常见算法有 Stoer-Wagner 等。

有向图常见连通性问题有：强连通分量、最小点基、最小权点基、2-SAT 问题 等。

强连通分量：有向图中，强连通分量指任意两点互相可达、且无法再扩展的极大子图。常用 Kosaraju 或 Tarjan 算法快速求解。
最小点基：在有向图中，选出最少的顶点，使得从这些点能到达所有顶点。常用于控制系统、可达性分析等。
最小权点基：在最小点基的基础上，要求选中顶点的权值和最小，常见于带权有向图的优化问题。
2-SAT 问题：2-SAT 是每个约束只包含两个变量的布尔可满足性问题（如 $x \lor \lnot y$ ）。可用强连通分量算法在线性时间判断有无解，并给出解。