6.3 深度优先搜索
6.3 深度优先搜索
---1. 深度优先搜索简介
深度优先搜索算法(Depth First Search,简称 DFS):是一种用于遍历或搜索树、图等结构的经典算法。其核心思想是「沿一条路径尽可能深入」,遇到无法继续的节点时再回溯到上一个分叉点,继续探索其他路径,直到遍历完整个结构或找到目标为止。
深度优先的含义,就是每次优先选择一条路径一直走到底,只有在无法继续时才回退,尝试其他分支。
在 DFS 的遍历过程中,我们通常需要暂存当前节点 的相邻节点,以便回溯时继续访问未遍历的节点。由于遍历顺序具有「后进先出」的特性,DFS 可以通过递归(系统栈)或显式使用栈结构来实现。
2. 深度优先搜索算法步骤
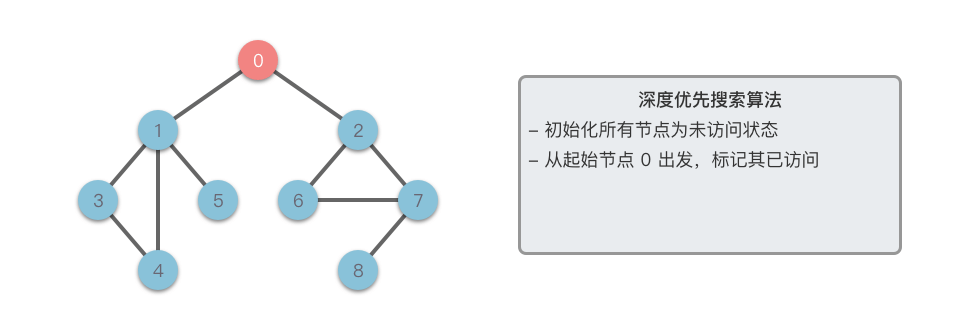
下面以无向图为例,简要梳理深度优先搜索的基本流程:
- 选定起始节点 ,将其标记为已访问。
- 判断当前节点 是否为目标节点(具体依据题目要求)。
- 如果 为目标节点,直接返回结果。
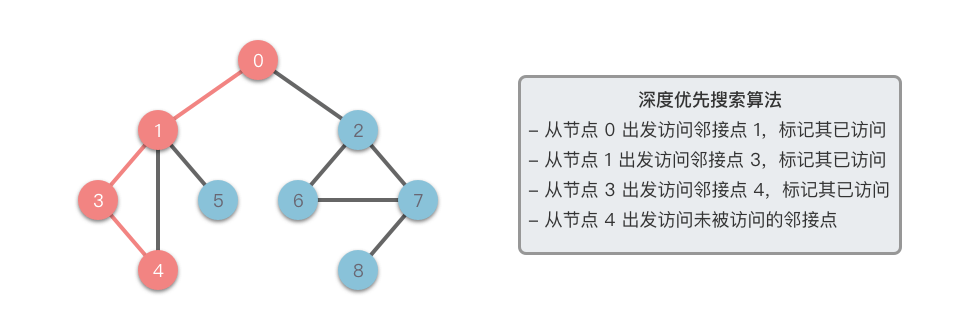
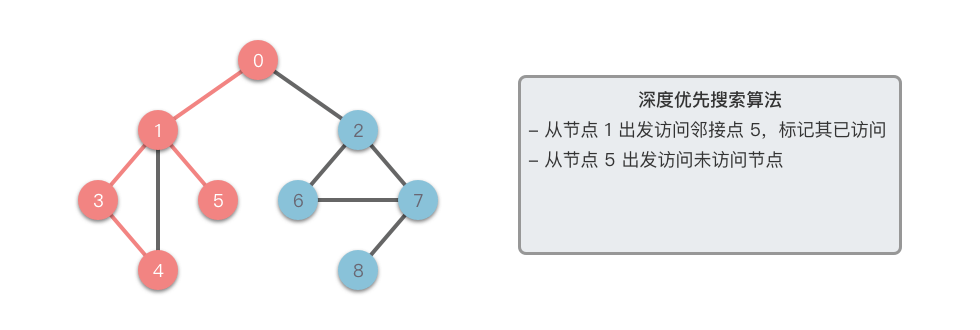
- 如果 不是目标节点,则遍历 的所有未被访问的邻接节点。
- 对每一个未访问的邻接节点 ,递归地从 继续进行深度优先搜索。
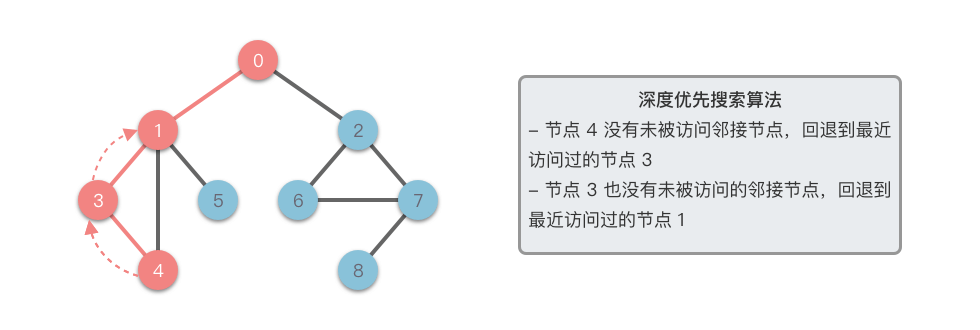
- 如果 没有未访问的邻接节点,则回溯到上一个节点,继续探索其他分支。
- 重复步骤 ,直到遍历完整个图或找到目标节点为止。
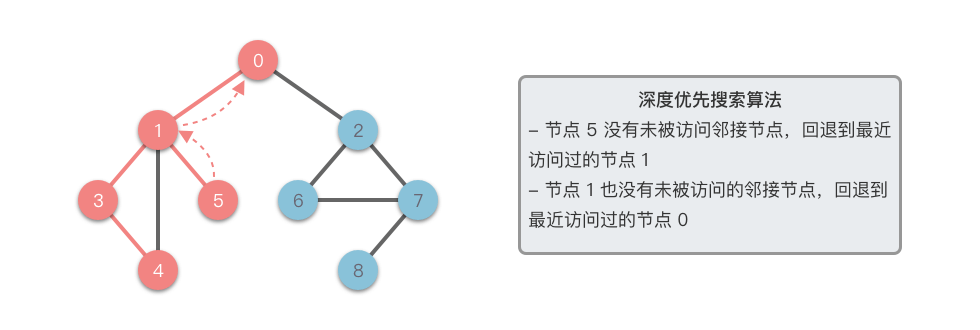
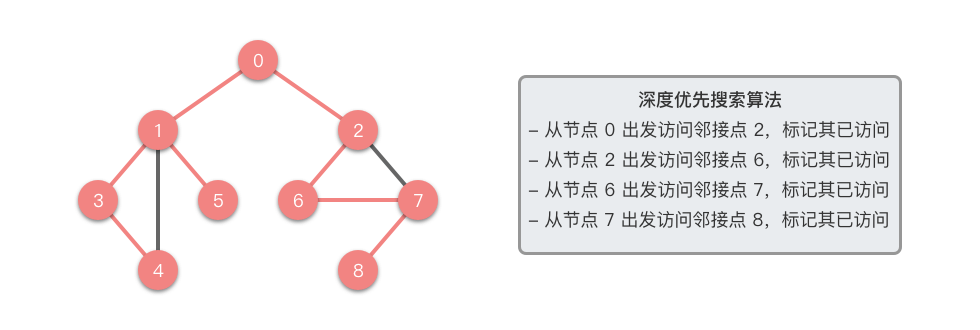
3. 基于递归的深度优先搜索
3.1 基于递归的深度优先搜索算法步骤
深度优先搜索(DFS)可以通过递归方式实现。其基本递归流程如下:
- 设 为无向图的邻接表, 为已访问节点的集合, 为当前节点。定义递归函数
def dfs_recursive(graph, u, visited):。 - 将起始节点 标记为已访问(
visited.add(u))。 - 判断当前节点 是否为目标节点(具体依据题目要求)。
- 如果 为目标节点,直接返回结果。
- 如果 不是目标节点,则遍历 的所有未访问的邻接节点 。
- 对每个未访问的邻接节点 ,递归调用
dfs_recursive(graph, v, visited)继续搜索。 - 如果 没有未访问的邻接节点,则自动回溯到上一个节点,继续探索其他分支。
- 重复步骤 ,直到遍历完整个图或找到目标节点为止。
3.2 基于递归的深度优先搜索实现代码
class Solution:
def dfs_recursive(self, graph, u, visited):
"""
递归实现深度优先搜索(DFS)
:param graph: 字典表示的邻接表,key为节点,value为邻接节点列表
:param u: 当前访问的节点
:param visited: 已访问节点的集合
"""
print(u) # 访问当前节点 u
visited.add(u) # 标记节点 u 已访问
# 遍历所有邻接节点
for v in graph[u]:
if v not in visited: # 如果邻接节点 v 未被访问
# 递归访问邻接节点 v
self.dfs_recursive(graph, v, visited)
# 示例图(邻接表形式,节点为字符串,边为无向边)
graph = {
"1": ["2", "3"],
"2": ["1", "3", "4"],
"3": ["1", "2", "4", "5"],
"4": ["2", "3", "5", "6"],
"5": ["3", "4"],
"6": ["4", "7"],
"7": []
}
# 初始化已访问节点集合
visited = set()
# 从节点 "1" 开始进行深度优先搜索
Solution().dfs_recursive(graph, "1", visited)4. 基于堆栈的深度优先搜索
4.1 基于堆栈的深度优先搜索算法步骤
除了递归方式,深度优先搜索(DFS)还可以用显式的栈结构实现。为避免重复访问同一节点,栈中不仅存储当前节点,还记录下一个待访问的邻接节点下标。这样每次出栈时,可以直接定位下一个邻接节点,无需遍历全部邻接点。
基于堆栈的 DFS 步骤如下:
- 设 为无向图的邻接表, 为已访问节点集合, 为辅助栈。
- 选择起始节点 ,检查当前节点 是否为目标节点(看具体题目要求)。
- 如果 是目标节点,直接返回结果。
- 如果 不是目标节点,将 (节点 及其下一个邻接节点下标 )压入栈,并将 标记为已访问:
stack.append([u, 0]),visited.add(u)。 - 当栈非空时,弹出栈顶元素 ,其中 表示下一个待访问的邻接节点下标。
- 如果 小于 的邻接节点数,则取出 。
- 将 压回栈中,表示下次将访问 的下一个邻接节点。
- 如果 未被访问,则对 进行相关操作(如打印、判定等),并将 压入栈,同时标记 已访问。
- 重复步骤 ,直到栈为空或找到目标节点为止。
这种实现方式可以模拟递归调用过程,且便于控制递归深度,适合递归层数较深或需手动管理回溯的场景。
4.2 基于堆栈实现的深度优先搜索实现代码
class Solution:
def dfs_stack(self, graph, u):
"""
基于显式栈的深度优先搜索(DFS),适用于无向图/有向图的邻接表表示。
:param graph: dict,邻接表,key为节点,value为邻接节点列表
:param u: 起始节点
"""
visited = set() # 记录已访问节点,防止重复遍历
stack = [] # 显式栈,模拟递归过程
stack.append([u, 0]) # 入栈:节点u及其下一个待访问邻接节点的下标 0
visited.add(u) # 标记起始节点已访问
print(u) # 访问起始节点
while stack:
cur, idx = stack.pop() # 取出当前节点及其下一个邻接节点下标
neighbors = graph[cur] # 当前节点的所有邻接节点
# 如果还有未遍历的邻接节点
if idx < len(neighbors):
v = neighbors[idx] # 取出下一个邻接节点
stack.append([cur, idx + 1]) # 当前节点下标 + 1,回溯时继续遍历下一个邻接点
if v not in visited:
print(v) # 访问新节点
visited.add(v) # 标记为已访问
stack.append([v, 0]) # 新节点入栈,准备遍历其邻接节点
# 也可以返回 visited 集合,便于后续处理
# return visited
# 示例图(邻接表形式,节点为字符串,边为无向边)
graph = {
"1": ["2", "3"],
"2": ["1", "3", "4"],
"3": ["1", "2", "4", "5"],
"4": ["2", "3", "5", "6"],
"5": ["3", "4"],
"6": ["4", "7"],
"7": []
}
# 从节点 "1" 开始进行深度优先搜索
Solution().dfs_stack(graph, "1")5. 深度优先搜索应用
5.1 岛屿数量
5.1.1 题目链接
5.1.2 题目大意
描述:给定一个由字符 '1'(陆地)和字符 '0'(水)组成的的二维网格 grid。
要求:计算网格中岛屿的数量。
说明:
- 岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
- 此外,你可以假设该网格的四条边均被水包围。
- 。
- 。
- 。
- 的值为
'0'或'1'。
示例:
- 示例 1:
输入:grid = [
["1","1","1","1","0"],
["1","1","0","1","0"],
["1","1","0","0","0"],
["0","0","0","0","0"]
]
输出:1- 示例 2:
输入:grid = [
["1","1","0","0","0"],
["1","1","0","0","0"],
["0","0","1","0","0"],
["0","0","0","1","1"]
]
输出:35.1.3 解题思路
本题实质是统计二维网格中「上下左右」相连的 '1' 组成的连通块数量,即岛屿的个数。
可以采用深度优先搜索(DFS)或广度优先搜索(BFS)来实现。
思路 1:深度优先搜索
- 遍历整个 网格。
- 当遇到字符为
'1'的格子时,说明发现了新的岛屿,执行深度优先搜索(DFS):- 将当前格子标记为
'0',避免重复访问。 - 递归访问其上下左右四个相邻格子(即 、、、)。
- 如果递归过程中遇到越界或当前格子为
'0',则直接返回。
- 将当前格子标记为
- 每当一次完整的 DFS 结束,岛屿计数加一。
- 最终 DFS 执行的次数即为岛屿的总数。
思路 1:代码
class Solution:
def dfs(self, grid, i, j):
n = len(grid)
m = len(grid[0])
if i < 0 or i >= n or j < 0 or j >= m or grid[i][j] == '0':
return 0
grid[i][j] = '0'
self.dfs(grid, i + 1, j)
self.dfs(grid, i, j + 1)
self.dfs(grid, i - 1, j)
self.dfs(grid, i, j - 1)
def numIslands(self, grid: List[List[str]]) -> int:
count = 0
for i in range(len(grid)):
for j in range(len(grid[0])):
if grid[i][j] == '1':
self.dfs(grid, i, j)
count += 1
return count思路 1:复杂度分析
- 时间复杂度:。其中 和 分别为行数和列数。
- 空间复杂度:。
5.2 克隆图
5.2.1 题目链接
5.2.2 题目大意
描述:以每个节点的邻接列表形式(二维列表)给定一个无向连通图,其中 表示值为 的节点的邻接列表, 表示值为 的节点与值为 的节点有一条边。
要求:返回该图的深拷贝。
说明:
- 节点数不超过 。
- 每个节点值 都是唯一的,。
- 无向图是一个简单图,这意味着图中没有重复的边,也没有自环。
- 由于图是无向的,如果节点 是节点 的邻居,那么节点 也必须是节点 的邻居。
- 图是连通图,你可以从给定节点访问到所有节点。
示例:
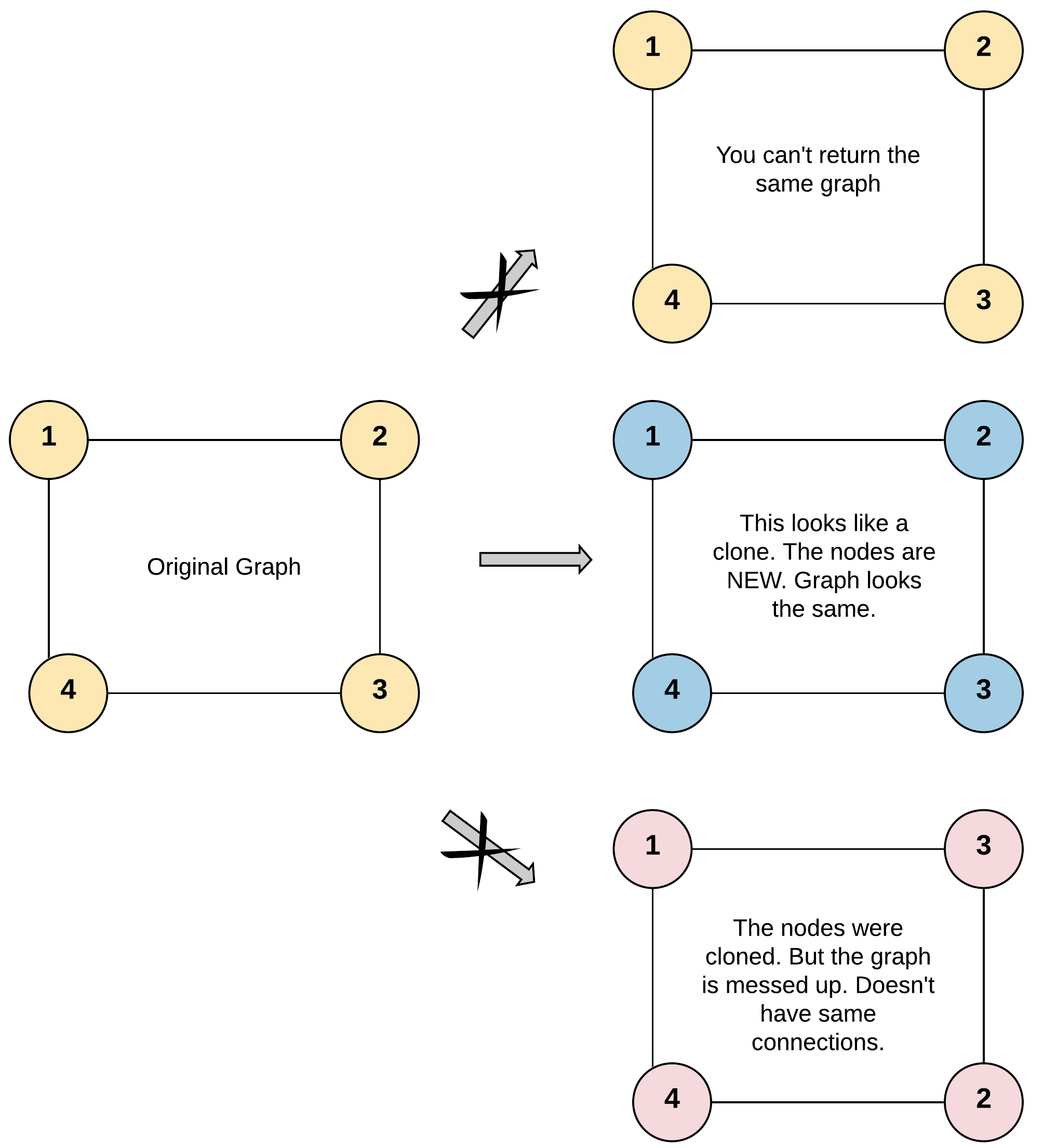
输入:adjList = [[2,4],[1,3],[2,4],[1,3]]
输出:[[2,4],[1,3],[2,4],[1,3]]
解释:
图中有 4 个节点。
节点 1 的值是 1,它有两个邻居:节点 2 和 4 。
节点 2 的值是 2,它有两个邻居:节点 1 和 3 。
节点 3 的值是 3,它有两个邻居:节点 2 和 4 。
节点 4 的值是 4,它有两个邻居:节点 1 和 3 。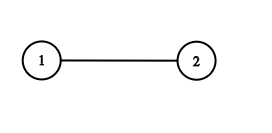
输入:adjList = [[2],[1]]
输出:[[2],[1]]5.2.3 解题思路
所谓深拷贝,就是构建一张与原图结构、值均一样的图,但是所用的节点不再是原图节点的引用,即每个节点都要新建。
可以用深度优先搜索或者广度优先搜索来做。
思路 1:深度优先搜索
- 使用哈希表 记录原图节点与其对应的克隆节点,键为原图节点,值为克隆节点。
- 从给定节点出发,采用深度优先搜索遍历原图:
- 如果当前节点已在哈希表中,直接返回对应的克隆节点,避免重复克隆。
- 如果当前节点未被访问,则新建一个克隆节点,并将其加入哈希表。
- 遍历当前节点的所有邻居,对每个邻居递归调用克隆函数,并将返回的克隆节点加入当前克隆节点的邻居列表。
- 递归返回当前节点的克隆节点。
思路 1:代码
class Solution:
def cloneGraph(self, node: 'Node') -> 'Node':
if not node:
return node
visitedDict = dict()
def dfs(node: 'Node') -> 'Node':
if node in visitedDict:
return visitedDict[node]
clone_node = Node(node.val, [])
visitedDict[node] = clone_node
for neighbor in node.neighbors:
clone_node.neighbors.append(dfs(neighbor))
return clone_node
return dfs(node)思路 1:复杂度分析
- 时间复杂度:。其中 为图中节点数量。
- 空间复杂度:。