6.6 最小生成树
6.6 最小生成树
---1. 最小生成树的定义
在介绍「最小生成树」之前,先来理解什么是「生成树」。
生成树(Spanning Tree):对于一个无向连通图 ,如果它的一个子图既包含 的所有顶点,又是一棵树(即连通且无环),那么这个子图就叫做 的生成树。生成树不是唯一的,从不同的顶点出发遍历,可能得到不同的生成树。
简单来说,生成树就是原图的一个子图,既要包含所有顶点,又要用尽量少的边把这些顶点连起来,并且不能有环。
生成树有以下几个显著特点:
- 包含所有顶点:生成树必须覆盖原图的所有顶点。
- 连通性:生成树是连通的,任意两个顶点之间都能互相到达。
- 无环性:生成树中没有环。
- 边数最少:生成树的边数总是等于顶点数减 ,即 条边。
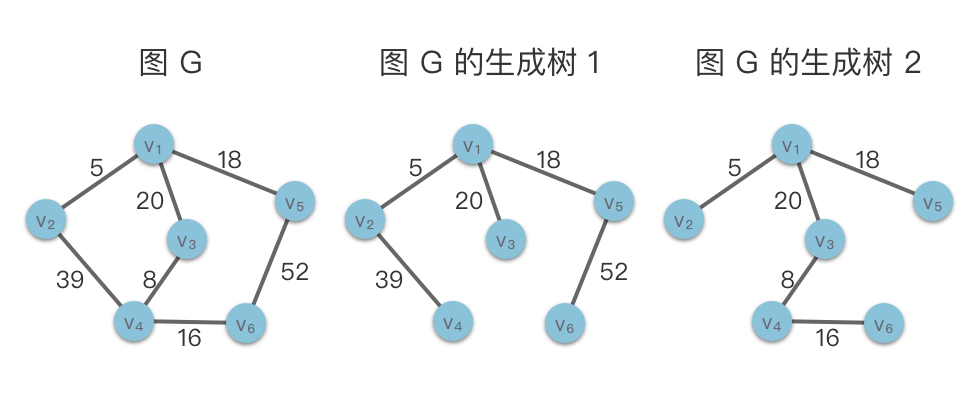
如上图,左边是一个有 个顶点、 条边的无向图 。右边展示了 的两棵不同的生成树,每棵都包含 个顶点和 条边。
最小生成树(Minimum Spanning Tree, MST):在所有可能的生成树中,边的权值之和最小的那一棵,就叫做最小生成树。
最小生成树除了具备生成树的所有性质外,还有一个最重要的特点:
- 边权和最小:在所有生成树中,最小生成树的边权之和最小。

如上图,左边是原始带权无向图 ,右边是 的最小生成树,既包含所有顶点,也只有 条边,并且所有边的权值加起来最小。
常用的两种最小生成树算法:
- Prim 算法:从任意一个顶点出发,每次选择一条连接已选顶点集合和未选顶点集合之间权值最小的边,直到所有顶点都被包含。
- Kruskal 算法:把所有边按权值从小到大排序,依次选择不会形成环的最小边,直到选够 条边。
这两种算法都能有效地帮助我们找到无向图的最小生成树,实现用最小的代价连接所有顶点。
2. Prim 算法
2.1 Prim 算法的核心思想
Prim 算法的核心思想:每次从当前已选顶点集合出发,选择一条连接到未选顶点、且权值最小的边,把对应的顶点和边加入生成树。这样不断扩展,直到所有顶点都被包含,最终得到边权和最小的生成树。
2.2 Prim 算法的实现步骤
- 首先,把所有顶点分成两组:一组是已经加入生成树的顶点集合 ,另一组是还未加入的顶点集合 。
- 随便选一个起点 ,把它加入 。
- 每次在 中找一个顶点 ,从 出发,挑选一条连接 和 的最小权值边。
- 把这条边和它连接的顶点一起加入生成树(即 ),并更新集合。
- 重复第 、 步,直到所有顶点都被加入生成树为止。
这样,Prim 算法就能一步步用最小的代价把所有顶点连起来,得到最小生成树。
2.3 Prim 算法的代码实现
class Solution:
# Prim 算法实现,graph 为邻接表(dict of dict),start 为起始顶点编号
def Prim(self, graph, start):
size = len(graph)
vis = set() # 已经加入最小生成树的顶点集合
dist = [float('inf')] * size # dist[i] 表示当前未加入集合的点 i 到已选集合的最小边权
ans = 0 # 最小生成树的总权值
dist[start] = 0 # 起点到自身距离为 0
# 初始化 dist 数组:起点到其他点的距离
for i in range(size):
if i != start:
dist[i] = graph[start][i]
vis.add(start) # 起点加入已访问集合
for _ in range(size - 1): # 还需加入 size-1 个顶点
min_dis = float('inf')
min_dis_pos = -1
# 在未访问的顶点中,选择距离已选集合最近的顶点
for i in range(size):
if i not in vis and dist[i] < min_dis:
min_dis = dist[i]
min_dis_pos = i
if min_dis_pos == -1: # 图不连通,无法生成最小生成树
return -1
ans += min_dis # 累加边权
vis.add(min_dis_pos) # 新顶点加入集合
# 用新加入的顶点更新其他未访问顶点的最小边权
for i in range(size):
if i not in vis and dist[i] > graph[min_dis_pos][i]:
dist[i] = graph[min_dis_pos][i]
return ans
# 示例:使用 Prim 算法计算最小生成树的权值和
# 构造一个点集,生成邻接矩阵(曼哈顿距离),并求最小生成树
points = [[0, 0]]
graph = dict()
size = len(points)
for i in range(size):
x1, y1 = points[i]
for j in range(size):
x2, y2 = points[j]
dist_ij = abs(x2 - x1) + abs(y2 - y1) # 曼哈顿距离
if i not in graph:
graph[i] = dict()
if j not in graph:
graph[j] = dict()
graph[i][j] = dist_ij
graph[j][i] = dist_ij # 无向图,双向赋值
# 调用 Prim 算法,输出最小生成树的权值和
print(Solution().Prim(graph, 0))2.4 Prim 算法复杂度分析
Prim 算法的时间复杂度主要由以下两部分构成:
初始化阶段:
- 初始化距离数组和访问集合,时间复杂度为 ,其中 表示顶点数。
主循环阶段:
- 外层循环共执行 次,每次选择一条边加入生成树。
- 每次循环需:
- 在线性扫描中找到未访问顶点中距离最小的顶点,复杂度为 。
- 遍历所有顶点,更新距离数组,复杂度为 。
综上,Prim 算法的总时间复杂度为 ,空间复杂度为 ,主要用于存储距离数组和访问集合。
3. Kruskal 算法
3.1 Kruskal 算法的核心思想
Kruskal 算法的核心思想:每次选择当前权重最小的边,判断这条边连接的两个顶点是否已经在同一个连通块(集合)中。如果不在同一个集合,就把这条边加入最小生成树,并把两个集合合并;如果已经在同一个集合,则跳过这条边,避免成环。如此反复,直到最小生成树包含了 条边。
在实际实现时,我们通常用「并查集」这种数据结构来高效管理集合的合并与查询操作,快速判断两个顶点是否属于同一个集合。
3.2 Kruskal 算法的实现步骤
- 把图中所有的边按照权重从小到大排序。
- 初始化时,每个顶点自成一个集合。
- 按照排序后的顺序,依次遍历每一条边。
- 对于每条边,判断它连接的两个顶点是否属于同一个集合:
- 如果属于同一个集合,说明这条边会形成环,跳过不选。
- 如果不属于同一个集合,就把这条边加入最小生成树,并把两个集合合并。
- 重复第 3、4 步,直到最小生成树中有 条边( 为顶点数),算法结束。
这样就能保证生成的树没有环,并且总权值最小。
3.3 Kruskal 算法的代码实现
class UnionFind:
def __init__(self, n):
# 初始化每个节点的父节点为自己
self.parent = [i for i in range(n)]
# 连通分量数量
self.count = n
def find(self, x):
# 查找根节点
while x != self.parent[x]:
self.parent[x] = self.parent[self.parent[x]]
x = self.parent[x]
return x
def union(self, x, y):
# 合并两个集合
root_x = self.find(x)
root_y = self.find(y)
if root_x == root_y:
return False # 已经在同一个集合,无需合并
self.parent[root_x] = root_y
self.count -= 1
return True # 合并成功
def is_connected(self, x, y):
# 判断两个节点是否属于同一个集合
return self.find(x) == self.find(y)
class Solution:
def Kruskal(self, edges, size):
"""
edges: 边集合,每条边为 [u, v, w],表示 u-v 权重为 w
size: 顶点数量
返回最小生成树的权值和
"""
union_find = UnionFind(size)
# 按权重升序排序所有边
edges.sort(key=lambda x: x[2])
ans = 0 # 最小生成树的总权值
edge_count = 0 # 已加入生成树的边数
for u, v, w in edges:
# 如果 u 和 v 不连通,则选这条边
if union_find.union(u, v):
ans += w
edge_count += 1
# 最小生成树边数为 n - 1 时结束
if edge_count == size - 1:
break
return ans
# 示例:使用 Kruskal 算法计算最小生成树的权值和
# 假设有 4 个顶点,边集如下(每条边为 [u, v, w],u 和 v 为顶点编号,w 为权重):
edges = [
[0, 1, 1],
[0, 2, 3],
[1, 2, 1],
[1, 3, 4],
[2, 3, 2]
]
size = 4 # 顶点数量
# 调用 Kruskal ,输出最小生成树的权值和
mst_weight = Solution().Kruskal(edges, size)
print("最小生成树的权值和为:", mst_weight)
# 输出:最小生成树的权值和为:43.4 Kruskal 算法复杂度分析
Kruskal 算法的时间和空间复杂度分析如下:
边的排序:对 条边按权重排序,时间复杂度为 。
并查集操作:
- 查找(find)和合并(union)操作的均摊时间复杂度均为 ,其中 为阿克曼函数的反函数,增长极慢,实际应用中可视为常数。
遍历边集:遍历所有边,时间复杂度为 。
综上,Kruskal 算法的总时间复杂度为 ,其中 为边数。空间复杂度为 , 为顶点数,主要用于并查集的数据结构。